Funzione primitiva

La primitiva F(x) di una funzione reale f(x) è un insieme di funzioni ( o famiglia di funzioni ) che hanno la derivata prima F'(x) uguale a f(x) per ogni valore di x del dominio.

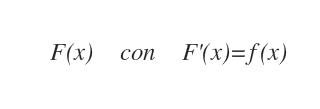
Esempio. La funzione reale f(x)=2x può essere ottenuta derivando la funzione F(x)=x². La derivata prima di F'(x) è 2x. Quindi, la funzione F(x) è una funzione primitiva di f(x).

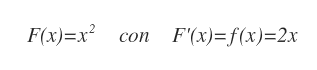
Le funzioni f(x) che hanno una primitiva sono dette funzioni integrabili.

Quando una funzione f(x) è integrabile, vuol dire che è la derivata di un'altra funzione F(x).

Tutte le funzioni sono integrabili? No, non tutte le funzioni ammettono una primitiva e sono integrabili. Tuttavia, tutte le funzioni continue ammettono almeno una primitiva e sono integrabili.

Le primitive di una funzione

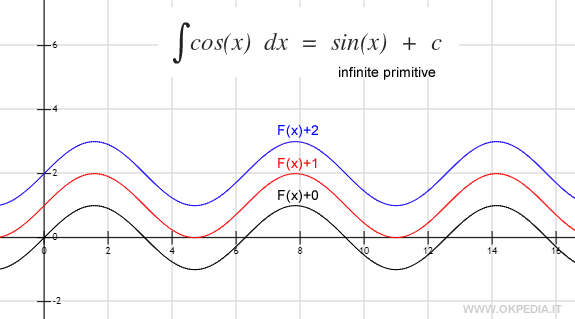
Una qualsiasi funzione reale f(x) non ha soltanto una primitiva bensì infinite primitive, perché può essere ottenuta derivando infinite funzioni che differiscono tra loro soltanto per una costante d.

Ad esempio, la funzione f(x)=2x ha come primitiva F(x)=x² perché la derivata prima F'(x) è uguale a 2x.

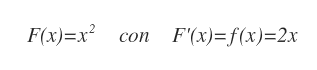
Tuttavia, anche la derivata della funzione F(x)=x²+1 è una primitiva di f(x) perché la derivata prima di una costante è uguale a zero.

Lo stesso vale per F(x)=x²+2. E così via.

Quindi, se F(x) è una primitiva di f(x) lo sono anche tutte le infinite funzioni F(x)+c che differiscono tra loro soltanto per una costante (c).

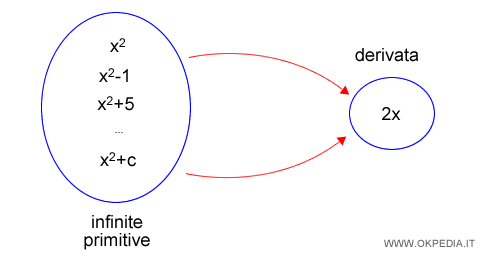
Teorema. Se una funzione f(x) ammette almeno una primitiva F(x), allora tutte le funzioni F(x)+c sono primitive della f(x), dove c è un numero reale qualsiasi.

Si può quindi affermare che una funzione f(x) può avere infinite primitive oppure nessuna.

Per questa ragione è sufficiente calcolare una sola primitiva F(x) di una funzione per conoscerle tutte F(x)+c.

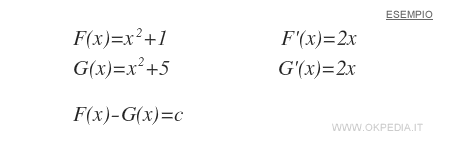
Teorema. Se due funzioni F(x) e G(x) sono primitive della stessa funzione f(x), allora le due funzioni differiscono tra loro per una costante c.

Dal punto di vista geometrico le funzioni primitive della stessa funzione sono traslazioni vertificali per ogni valore della costante reale c.

Come calcolare le primitive

Il calcolo delle primitive di una funzione si basa sul processo di integrazione.

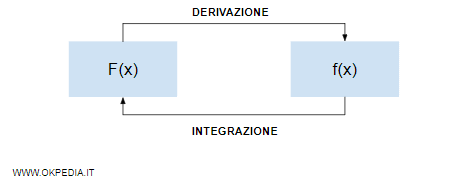
Cos'è l'integrazione? Nel calcolo infinitesimale l'integrazione è l'operazione opposta della derivazione di una funzione. Si ottiene tramite il calcolo dell'integrale indefinito.

Per calcolare la famiglia delle primitive della funzione f(x), si cercano tutte le funzioni F(x) con la derivata prima F'(x) uguale a f(x).

Un esempio pratico di integrazione

Data la funzione f(x)=x, la famiglia di primitive è composta dalle funzioni F(x)=1/2·x²+c, perché la derivata prima F'(x) di ognuna di queste è uguale a f(x)=x.

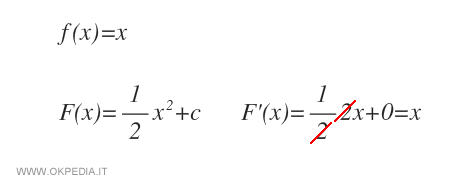
Il processo di integrazione si indica con la seguente notazione:

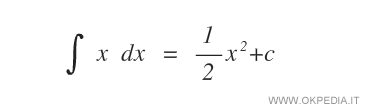
Lo stesso procedimento può essere calcolato per determinare le primitive di qualsiasi funzione.