Derivata di una funzione
In matematica una funzione reale f(x) è derivabile in un punto x0 del suo dominio se esiste ed è finito il limite del rapporto incrementale della funzione al tendere a zero dell'incremento Δx della variabile indipendente.
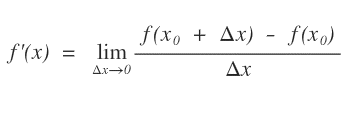
Tale limite è detto derivata o funzione derivata di f(x) e si indica con f'(x).
La spiegazione della derivata
La nozione di derivata di una funzione viene affrontata per la prima volta dal matematico francese Fermat nel XVII secolo.
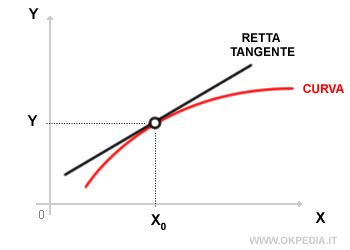
Fermat cerca di calcolare l'inclinazione ( coefficiente angolare ) della retta tangente nel punto x0 di una curva.
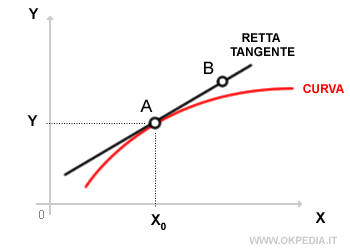
Per calcolare il coefficiente angolare della retta è sufficiente conoscere almeno due punti della retta ( es. A e B ).
Il rapporto incrementale tra i segmenti BC e AC determina il coefficiente angolare ossia l'inclinazione della retta tangente nel punto X0.
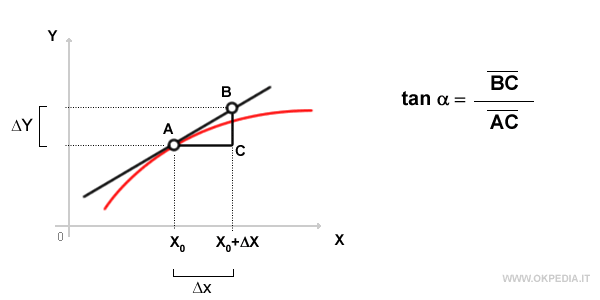
Perché si dice rapporto incrementale? Il rapporto tra i segmenti BC e AC è detto rapporto incrementale della retta perché misura il rapporto ΔY/ΔX ossia il tra l'incremento della variabile dipendente ΔY ( segmento BC ) e l'incremento della variabile indipendente ΔX ( segmento AC ).
Tuttavia, se si conosce un solo punto della retta tangente (X0) quest'ultimo procedimento di calcolo non è possibile.
Si può però calcolare il coefficiente angolare della retta tangente in X0 tramite il rapporto incrementale della funzione f(x).
Dato un qualsiasi incremento ΔX della variabile dipendente, si calcola il rapporto incrementale ΔY/ΔX della funzione f(x).
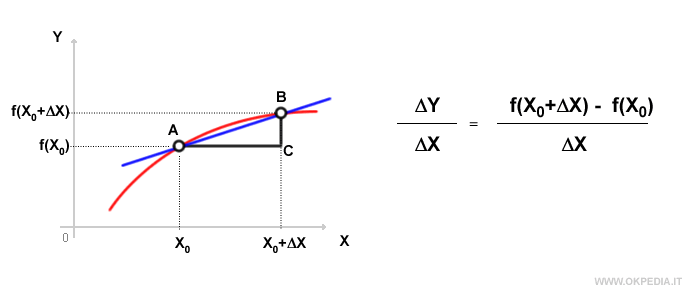
Si individua così una retta secante nei punti A e B con inclinazione ΔY/ΔX.
Facendo tendere a zero l'incremento ΔX, il coefficiente angolare della retta secante si avvicina progressivamente all'inclinazione della retta tangente nel punto X0.
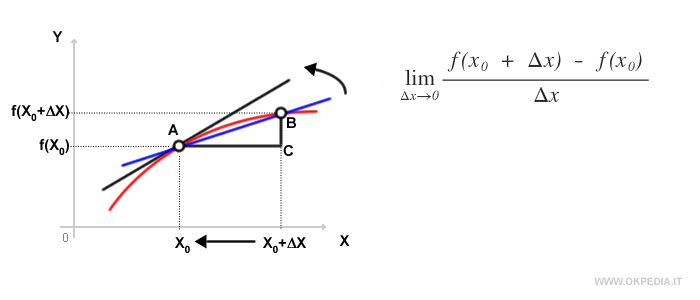
Pertanto, il limite del rapporto incrementale della funzione f(x) per ΔX che tende a zero, eguaglia il coefficiente angolare della retta tangente alla curva nel punto X0.
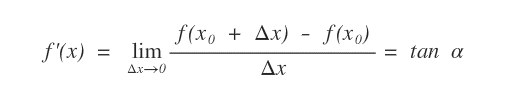
In questo modo è possibile calcolare l'inclinazione della retta tangente alla curva nel punto X0 anche se si conosce un solo punto della retta.
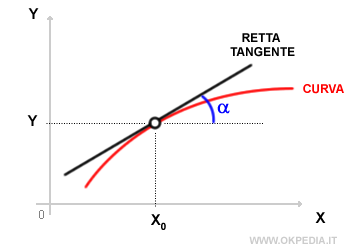
Il valore numerico del coefficiente angolare è uguale alla tangente trigonometrica dell'angolo α compreso tra la retta e l'asse delle ascisse (x).
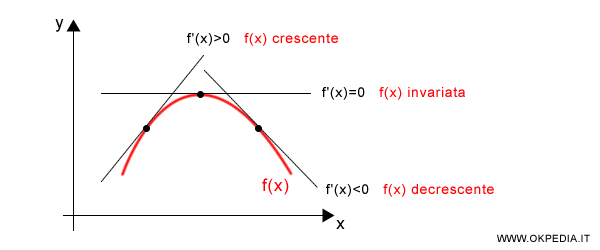
Lo studio del segno della derivata in un punto. Dallo studio del segno della derivata di f(x) in un punto x0 si può capire facilmente se la funzione è crescente, decrescente o costante in quel punto. Se il numeratore ΔY del rapporto incrementale è un numero positivo, la funzione f(x) è sicuramente crescente. Se il numeratore ΔY è negativo, allora la funzione f(x) è sicuramente decrescente. Se ΔY è nullo, la funzione è costante.
Il differenziale
Quando gli incrementi ΔX e ΔY diventano infinitesimali sono indicati rispettivamente con la notazione dx e dy detta differenziale.
Pertanto, la derivata di una funzione può essere scritta nel seguente modo:
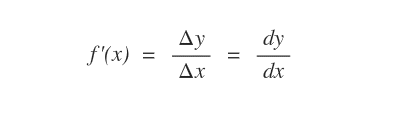
Lo studio degli incrementi infinitesimali è detto calcolo infinitesimale.
Nota. Se una funzione ammetta una derivata finita in un punto, in quel punto la funzione è sicuramente continua.
La funzione derivata
La funzione derivata è la funzione che, se esiste, associa a ogni punto x il valore della derivata della funzione primitiva f(x).
E' indicata con la notazione f'(x) oppure Df(x).
Nota. La derivata di una funzione f(x) è detta derivata prima f'(x). La derivata della funzione prima è detta derivata seconda ed è indicata con la notazione f"(x).
La derivata di ordine superiore
La derivata di ordine superiore è la derivata di una derivata.
Il processo di derivazione è sempre lo stesso ma si prende come funzione di partenza la funzione derivata f'(x).
Si dice derivata seconda la derivata di una derivata prima.
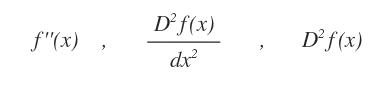
Esempio di calcolo della derivata seconda. Data una funzione f(x)=x2, la derivata prima è f'(x)=2x. La derivata seconda di f(x) è la derivata di f'(x) ossia f"(x)=2. Con lo stesso procedimento si può calcolare la derivata terza.
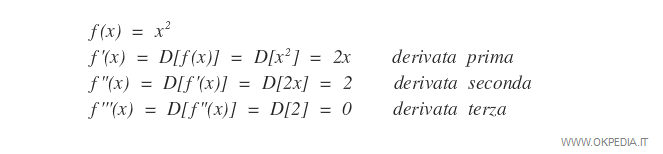
Si dice derivata terza la derivata della derivata seconda.
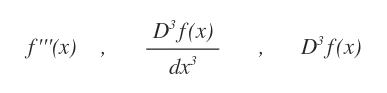
In modo analogo sono calcolate la derivata quarta, quinta e così via.
A cosa servono le derivate di ordine superiore? Le derivate di ordine superiori sono utili nello studio della funzione. Ad esempio, la derivata seconda consente di capire la concavità e la convessità della funzione.
