Analisi e studio della funzione

Il calcolo infinitesimale consente di studiare l'andamento di una funzione reale al variare della variabile indipendente (x) e all'interno del dominio dei numeri reali (R).

Il campo di esistenza della funzione

Il primo passo dell'analisi della funzione è la determinazione del campo di esistenza ( o dominio ) della funzione.

Come determinare il dominio della funzione

Si individua l'intervallo dei valori ( a, b ) della variabile indipendente (x) in cui la funzione y=f(x) ha significato e restituisce un risultato.

Esempio. La funzione 1/x è definita su tutto il campo di variazione dei numeri reali ad eccezione di x=0 perché nessun numero è divisibile per zero. Gli estremi del dominio sono +∞ e -∞.

Una volta individuato il campo di esistenza della funzione, si possono calcolare i limiti agli estremi e nei punti in cui la funzione è indefinita.

I limiti agli estremi del dominio

Lo studio del limite agli estremi del campo di esistenza consente di comprendere l'andamento della funzione.

Esempio. Gli estremi del campo di esistenza della funzione reale f(x)=1/x sono +∞ e -∞. Il limite della funzione per x tendente a +∞ è 0. Il limite della funzione per x tendente a -∞ è 0.

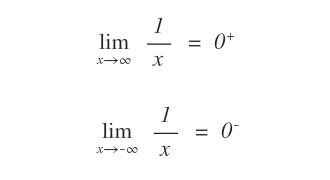
Il limite agli estremi può essere:

1. Un numero finito. Se il limite a un estremo della funzione è un numero finito l, la funzione tende al numero l.
   
   

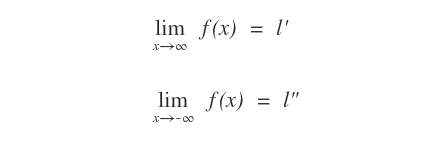
   Nota. Se l'estremo è +∞ o -∞ e il limite è un numero finito l allora si tratta di un asintoto orizzontale. Una funzione può avere al massimo due asintoti orizzontali per x→∞ e x→-∞.
   

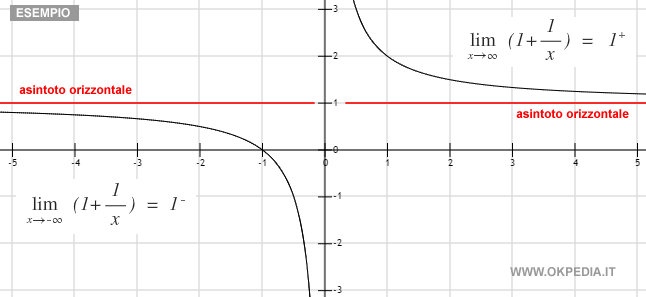
2. Infinito. Se il limite a un estremo della funzione è +∞ o - ∞, la funzione f(x) tende rispettivamente a +∞ o -∞ a quell'estremo.
   
   

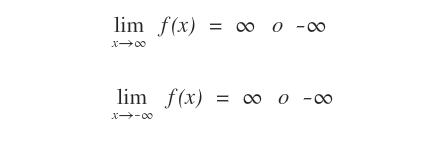
   Nota. Se l'estremo è +∞ o -∞ ed esiste il limite finito del rapporto f(x)/x=m e f(x)-mx=q, allora la funzione tende a un asintoto obliquo determinato dalla retta y=mx+q.
   

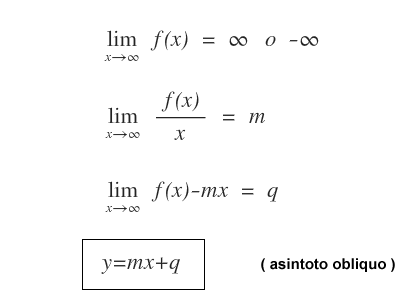
Il limite nei punti indefiniti della funzione

Se la funzione presenta dei punti c in cui è indefinita, Il limite per x→c consente di trovare eventuali asintoti verticali.

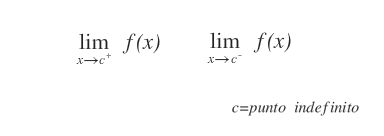
Una funzione può avere uno, nessuno o molti asintoti verticali.

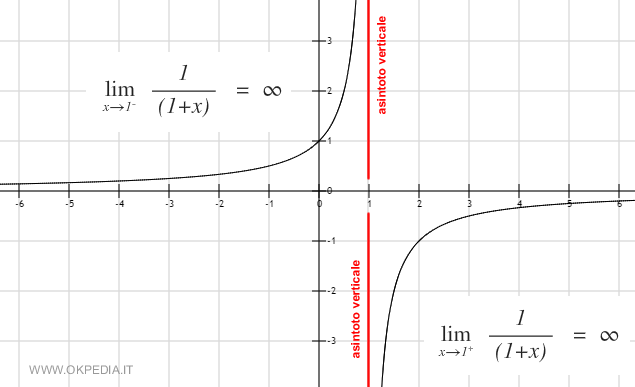
Esempio. La funzione 1(1-x) è indefinita in x=1. Calcolando il limite destro per x→1⁺ la funzione tende a -∞ e si individua un asintoto verticale negativo in x=1. Calcolando il limite sinistro per x→1^- la funzione tende a +∞ e si individua così un asintoto verticale positivo in x=1.

Lo studio del segno della funzione

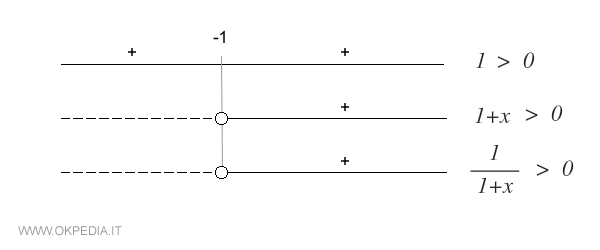
Lo studio del segno della funzione si ottiene risolvendo la disequazione f(x)>0.

Con l'analisi del segno della disequazione si individuano gli intervalli in cui la funzione è positiva e quelli in cui è negativa o nulla.

Esempio. Lo studio del segno della funzione f(x)=1/(1+x) individua l'intervallo (-1, +∞) in cui f(x)>0.

Le intersezioni con gli assi

Un'altra informazione utile per costruire il grafico della funzione sono le intersezioni con gli assi del diagramma cartesiano.

L'intersezione con le ordinate (y)

Per trovare l'intersezione con l'asse delle ordinate (y) si pone a zero la variabile indipendente della funzione (x=0).

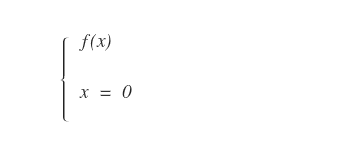
In questo modo si trova il valore corrispondente della variabile dipendente (y) quando x=0.

Esempio. La funzione f(x)=(2-x) ha un intercetta con l'asse delle ordinate alle coordinate ( 0, 2 ). Sostituendo il valore 0 alla variabile x si calcola il valore corrispondente della variabile y.

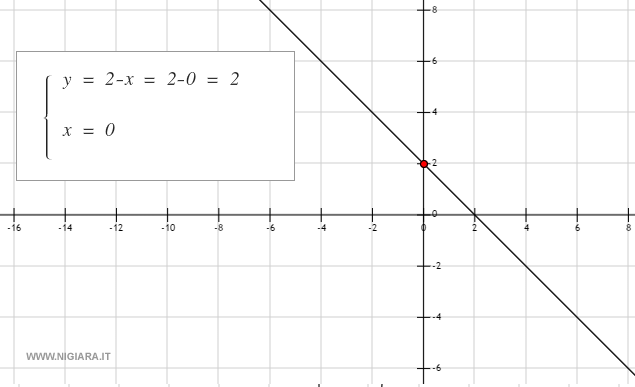
L'intersezione con le ascisse (x)

Per trovare l'intersezione con l'asse delle ascisse (x) si pone a zero la funzione f(x)=0 e si risolve l'equazione.

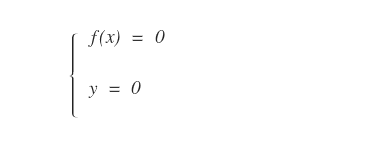
In questo modo si trova il valore corrispondente della variabile indipendente (x) quando y=0.

Esempio. La funzione f(x)=(2-x) ha un intercetta con l'asse delle ascisse alle coordinate ( 2, 0 ). Risolvendo l'equazione 2-x=0 si calcola il valore corrispondente della variabile y ossia x=2.

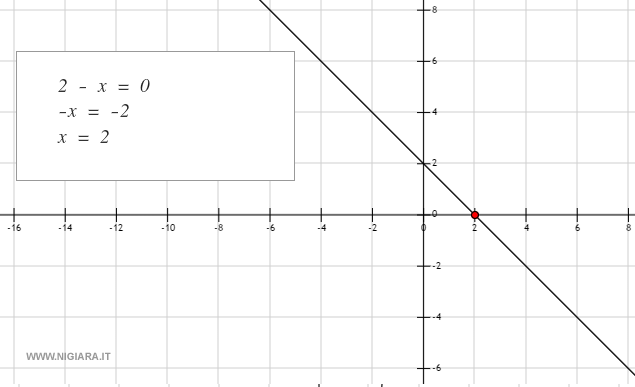
L'analisi della funzione con le derivate

La derivata di una funzione consente l'analisi e lo studio di una funzione. In particolar modo, la derivata prima permette di stabilire la crescenza o la decrescenza.

La derivata seconda, invece, consente di riconoscere la concavità e la convessità delle curve, i tratti rettilinei, i punti di massimo e di minimo, i flessi.

L'analisi della crescenza e della decrescenza

L'analisi della funzione derivata prima di una funzione f(x) consente di affermare se la funzione f(x) sta crescendo o decrescendo in un punto X, oppure è invariata.

1. Se la derivata prima f'(x) è positiva nel punto x, la funzione f(x) sta crescendo in x.
   
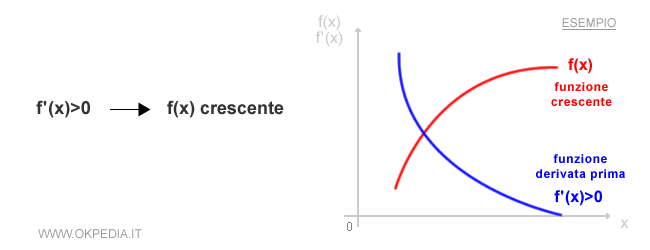
2. Se la derivata prima f'(x) è negativa nel punto x, la funzione f(x) sta decrescendo in x.
   
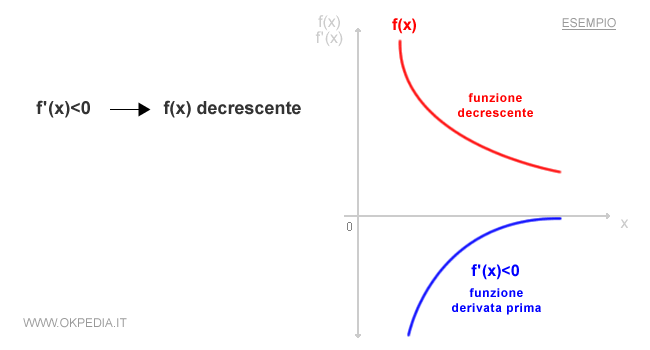
3. Se la derivata prima f'(x) è uguale a zero nel punto x, la funzione f(x) è invariata in x.
   

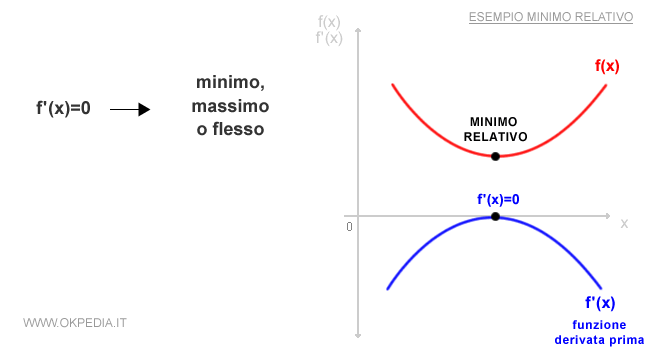
Minimo, massimo o flesso. I casi in cui la derivata è nulla sono detti punti stazionari e indicano che nel punto si sta verificando un punto di minimo, massimo, oppure un flesso.

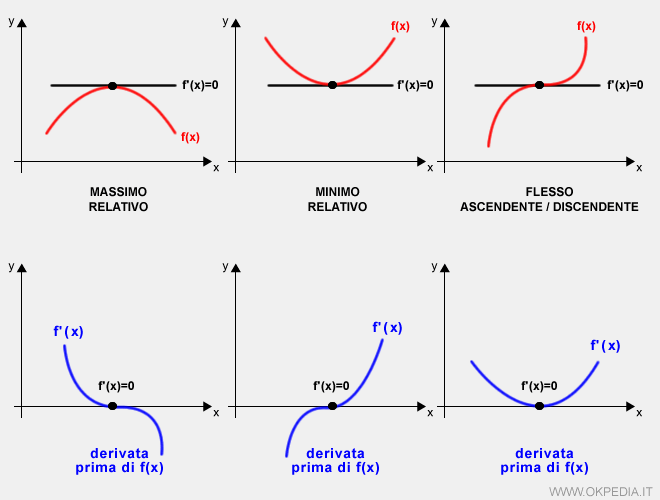
I punti di massimo, minimo e i flessi

Per individuare i punti di minimo, massimo e i flessi si studia l'intorno della derivata prima intorno ai punti stazionari.

Cos'è un punto stazionario? È un punto della funzione dove la derivata prima si annulla.

1. Massimo. Se l'intorno della derivata prima del punto X è positivo a sinistra e negativo a destra.
2. Minimo. Se l'intorno della derivata prima del punto X è negativo a sinistra e positivo a destra.
3. Flesso. Se nell'intorno del punto X la derivata prima f'(x) non cambia segno.

Derivata seconda: concavità, convessità

Lo studio della derivata seconda di una funzione f(x) consente di affermare se la funzione f(x) è convessa, concava o rettilinea nel punto X.

Cos'è la derivata seconda? La derivata seconda f"(x) è la derivata di una funzione derivata prima f'(x). Pertanto, è due volte la derivata della funzione originaria f(x).

1. Se la derivata seconda f"(x) è positiva nel punto x, la funzione f(x) è convessa in x.
   

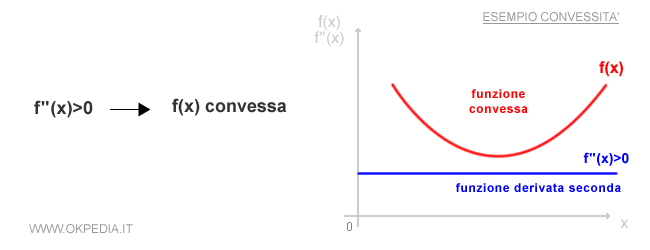
   Quando una curva è convessa? Una curva è convessa se dati due punti qualsiasi della curva, la retta che li congiunge è sempre al di sopra della curva. La convessità può essere definita anche come una concavità verso il basso.

2. Se la derivata seconda f''(x) è negativa nel punto x, la funzione f(x) è concava in x.
   

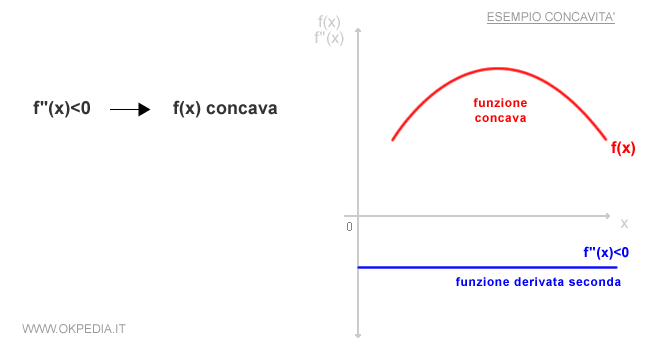
   Quando una funzione si dice concava? Una curva è concava se dati due punti qualsiasi la retta che li congiunge è sempre al dì sotto della curva. In questo caso la concavità è rivolta verso l'alto.

3. Se la derivata seconda f"(x) è nulla nel punto x, la funzione f(x) è rettilinea nel punto X, ha un flesso ascendente o discendente nel punto X oppure un massimo/minimo relativo.
   

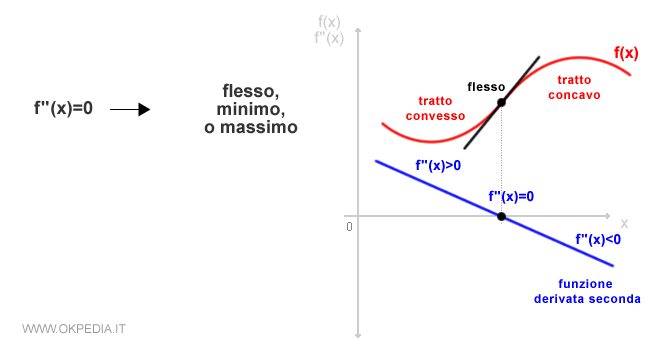
   Minimo, massimo o flesso. Se la derivata seconda è diversa da zero, il punto X è un massimo o minimo relativo. È un massimo relativo se è la derivata seconda è minore di zero oppure è un minimo relativo se è maggiore di zero. Se la derivata seconda è nulla, il punto X potrebbe essere un flesso ascendente o discendente oppure un punto di massimo o minimo relativo. Per capirlo occorre studiare il segno della funzione derivata seconda intorno a X oppure calcolare la derivata terza.
   
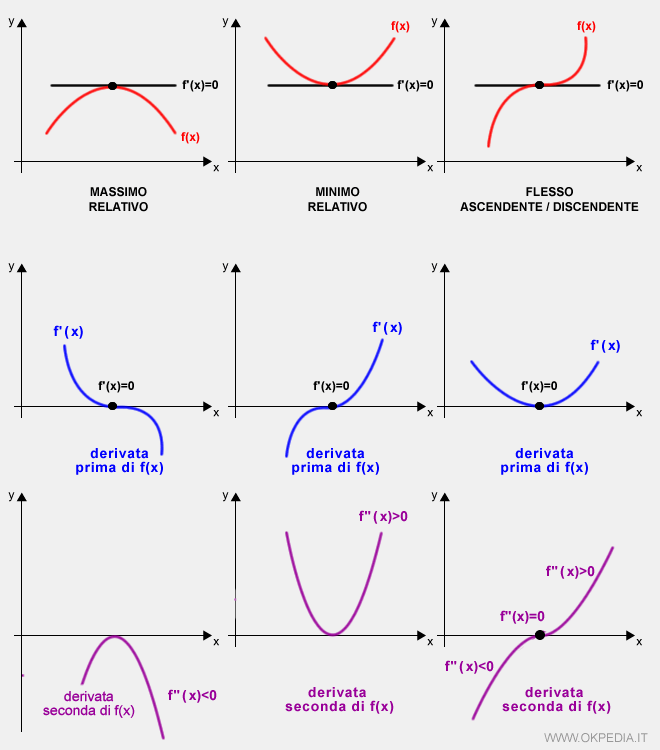
   Se la derivata seconda è nulla f''(x₀)=0, si verifica un flesso ascendente se la derivata seconda è crescente nell'intorno di x₀, oppure un flesso discendente se la derivata seconda è decrescente. Detto in altri termini, si rileva un flusso ascendente se la derivata terza è positiva f⁽³⁾(x₀)>0 oppure un flesso discendente se la derivata terza è negativa f⁽³⁾(x₀)<0.