Studio della funzione ( esempio )
In questo esempio di analisi della funzione si studia la funzione 1-x2.
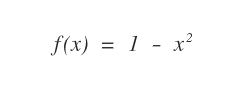
Il campo di esistenza della variabile indipendente x ( o dominio ) della funzione è l'insieme dei numeri reali da -∞ a +∞.
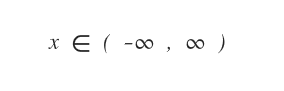
Si calcola il limite agli estremi del dominio ( -∞ e +∞ ) per studiare l'andamento della funzione.
La funzione tende a -∞ all'estremo di sinistra.
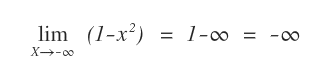
La funzione tende a -∞ anche all'estremo di destra.
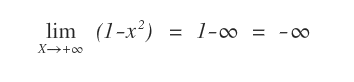
Nota. Non ci sono asintoti orizzontali a destra o a sinistra perché il valore del limite è infinito.
Non ci sono punti indefiniti nella funzione. Pertanto, non ci sono asintoti verticali.
Si procede a calcolare l'intervallo in cui la f(x)>0 risolvendo la disequazione.

Pertanto, la funzione è positiva nell'intervallo (-1,1).
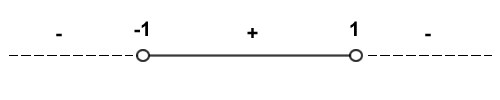
Ora si calcola l'intersezione con l'asse delle ordinate ponendo a zero la variabile X.
Il punto di intersezione con l'asse Y si trova alle coordinate ( 0 , 1 ).
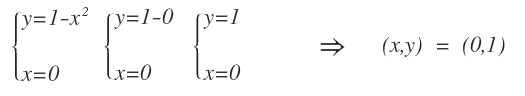
Poi si individua l'intersezione con l'asse delle ascisse risolvendo l'equazione 1-x2=0.
Esistono due punti di intersezione con l'asse X alle coordinate ( 1 , 0 ) e ( -1 , 0 ).
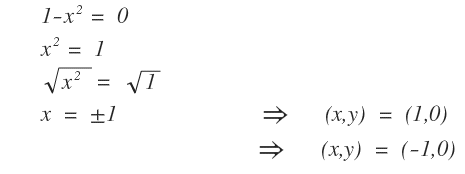
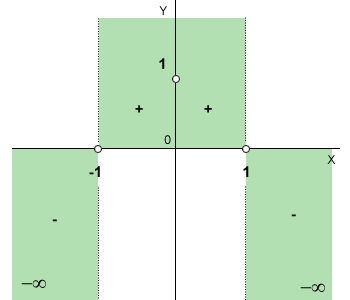
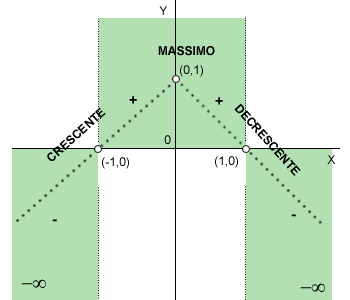
Con le informazioni ottenute ( intercette, limiti, segno ) è possibile disegnare la prima bozza del grafico della funzione.
La funzione esiste nelle aree evidenziate in verde del diagramma cartesiano.
A questo punto si calcola la derivata prima della funzione per studiare la crescenza e la decrescenza della funzione.
La derivata prima della funzione è f'(x)=-2x.
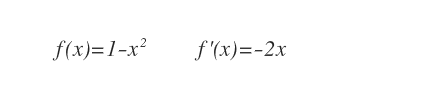
Tramite lo studio del segno della funzione derivata -2x si individuano gli intervalli di crescenza, decrescenza e i punti stazionari.
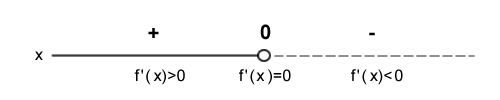
In questo caso
- la derivata è positiva f'(x)>0 quando x<0 ( crescenza )
- la derivata è negativa f'(x)<0 quando x>0 ( decrescenza )
- la derivata è nulla f'(x)=0 quando x=0 ( punto stazionario )
Quindi, nell'intervallo (-∞,0) la funzione è crescente mentre nell'intervallo (0, +∞) è decrescente.
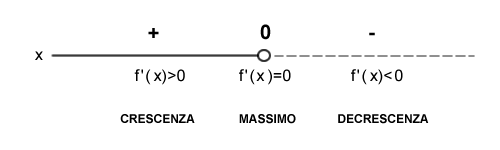
Nel punto x=0 invece si rileva un punto di massimo locale perché l'intorno della f'(x) è positivo a sinistra (funzione crescente) e negativo a destra (funzione decrescente).
Infine di calcola la derivata seconda della funzione per individuare i tratti di convessità e concavità del grafico.
La derivata seconda f"(x) è uguale a -2.
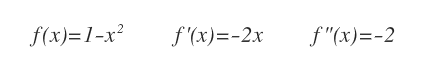
Analizzando il segno della funzione derivata seconda f"(x)=-2 si individuano gli intervalli di convessità quando f"(x)>0.
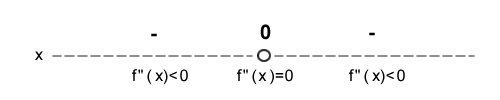
Essendo f"(x) una costante minore di zero (-2) su tutto il dominio, ad eccezione di x=0 ( massimo locale ), si può affermare che la funzione f(x) è concava in ogni suo punto.
Nota. Nei punti in cui la derivata seconda è nulla f"(x)=0 la funzione ha un massimo o un minimo locale. In questo caso sappiamo già che in x=0 la funzione ha un punto di massimo locale.
Pertanto il grafico della funzione è il seguente:
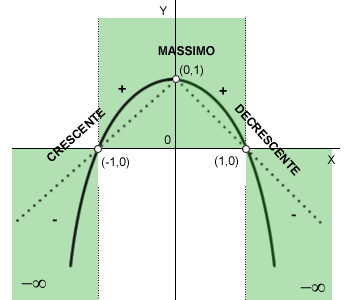
L'analisi della funzione si conclude con il disegno del grafico della funzione sul diagramma cartesiano.
