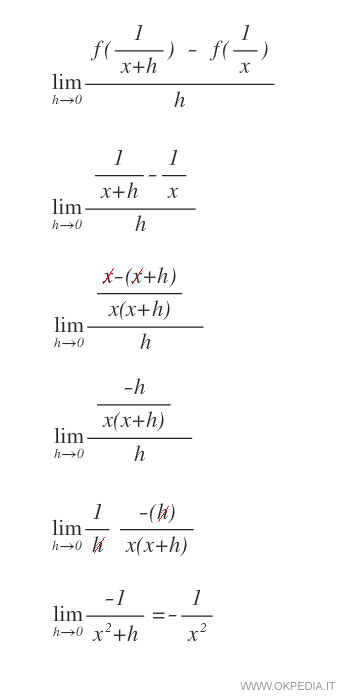Derivate di funzioni elementari
Ogni funzione elementare è associata a una e una sola funzione derivata. È un concetto alla base del calcolo differenziale.
Derivate di una funzione elementare
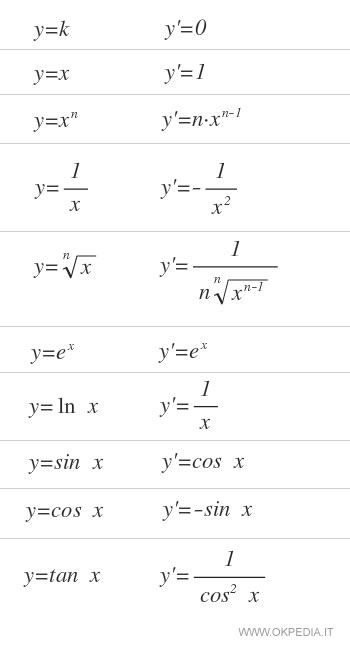
La precedente tabella mostra le derivate prime delle principali funzioni elementari f(x). È utile memorizzarla per svolgere più velocemente le operazioni del calcolo differenziale ( es. analisi di una funzione ).
Come viene calcolata la derivata di una funzione elementare? Nei prossimi paragrafi di questa pagina sono pubblicate le spiegazioni e le dimostrazioni matematiche del calcolo della derivata di una funzione elementare.
La derivata della funzione costante
Se la funzione elementare è composta soltanto da una costante k, la derivata è sempre uguale a zero.
Dimostrazione
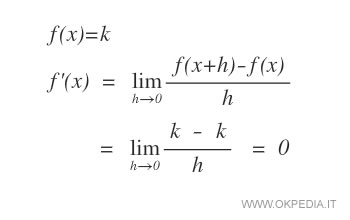
La derivata della funzione lineare
La derivata di una funzione f(x)=x è uguale a 1.
Dimostrazione
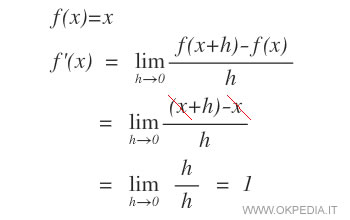
La derivata della potenza xn
La derivata della variabile X elevata a n è uguale a n·xn-1.
Dimostrazione
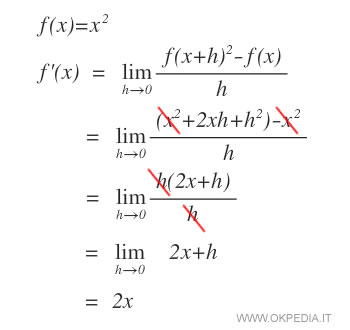
La derivata della radice
Una radice ennesima della variabile X può essere trasformata in una potenza di X elevata alla frazione 1/n. In questo modo si può applicare la formula della derivata di una potenza.
Dimostrazione
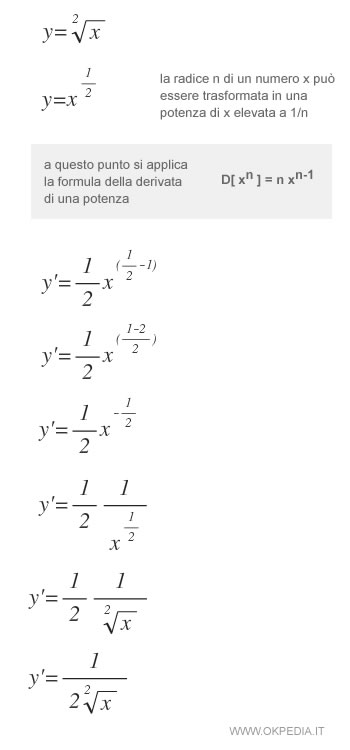
La derivata del reciproco
La derivata del reciproco può essere dimostrata in modo semplice considerando il reciproco come la potenza di un numero negativo.
Dimostrazione

Nota. Come ogni altra derivata anche quella del reciproco può essere dimostrata analizzando il limite che tende a zero del rapporto incrementale della funzione.