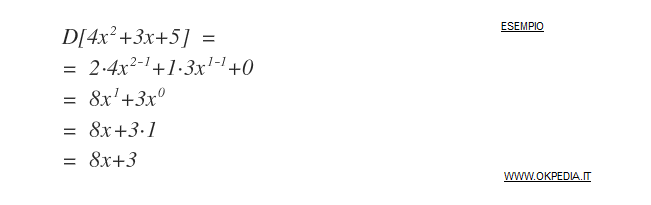Derivate complesse
Per derivare le funzioni complesse si utilizzano delle regole di derivazione che semplificano il calcolo dette "algebra delle derivate".
Cos'è una derivata complessa? Una derivata è detta complessa quando è composta da due funzioni f(x) e g(x) o dal prodotto tra una costante k e una funzione.
Le regole di derivazione sono classificate in base all'operazione algebrica tra le due funzioni ( divisione, moltiplicazione, addizione, ecc. ).
La derivata del prodotto di una costante per una funzione
La derivata del prodotto di una costante k per una funzione f(x) è uguale al prodotto della costante k per la derivata di f(x).
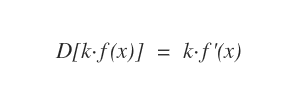
In questo caso la costante non si calcola la derivata della costante ma soltanto della funzione.
Esempio
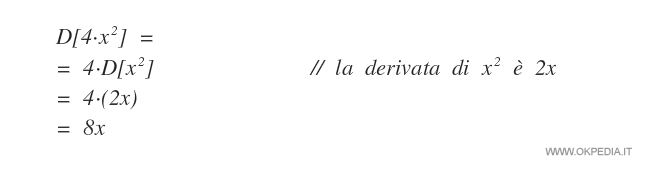
La derivata della somma di due funzioni
La derivata della somma di due funzioni f(x)+g(x) è uguale alla somma delle derivate delle due funzioni f'(x)+g'(x).
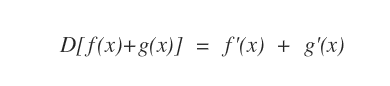
In questa regola di derivazione le funzioni sono derivate come funzioni semplici. La stessa regola si applica nella sottrazione di due funzioni.
Esempio
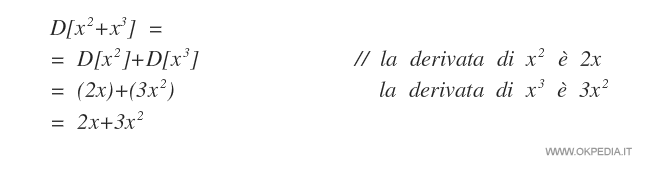
La derivata del prodotto di due funzioni
La derivata del prodotto di due funzioni [f(x)·g(x)] è uguale alla somma della derivata della prima funzione moltiplicata per la seconda funzione f'(x)·g(x) e della derivata della seconda funzione moltiplicata per la prima funzione f(x)·g'(x).
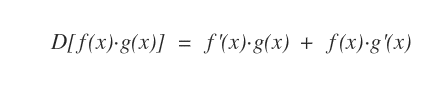
Esempio
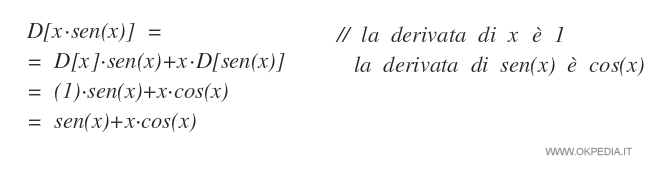
Nel caso di una moltiplicazione tra una funzione e una costante k·f(x), uno dei due membri si annulla perché la derivata di una costante è uguale a zero. Questo spiega la prima regola di derivazione.
La derivata del rapporto tra due funzioni
La derivata del rapporto tra due funzioni f(x)/g(x) è uguale alla seguente formula:
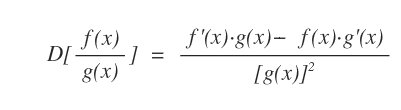
Esempio

La derivata della funzione composta
Una funzione composta è una funzione di funzione. La derivata della funzione composta f(g(x)) è uguale al prodotto delle derivate delle funzioni f'(x)·g'(x).
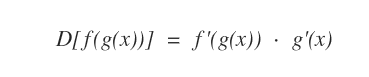
Esempio

La derivata di un polinomio
La regola di derivazione di un polinomio è la seguente:
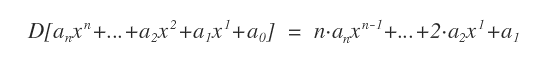
Esempio