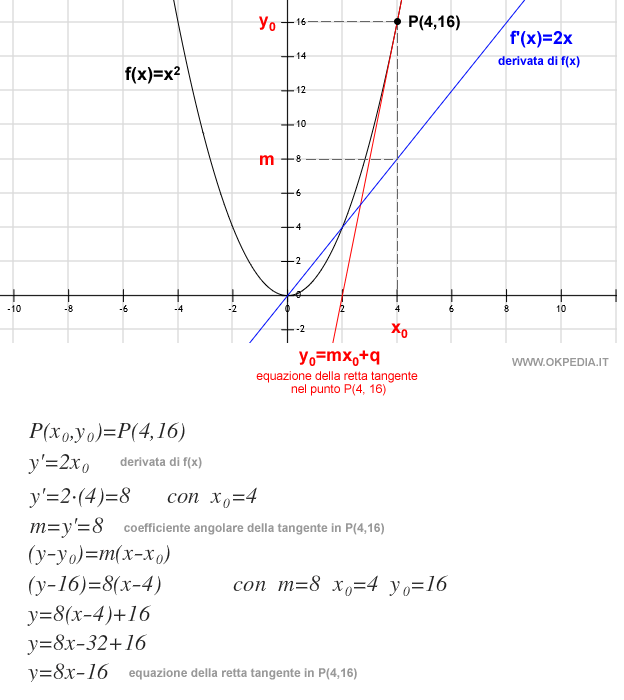
Esempio di derivata
Per comprendere il significato delle derivate è utile fare un esempio pratico.
Qual è lo scopo di una derivata? La derivata di una funzione consente di trovare la retta tangente in un qualsiasi punto della funzione.
Come trovare la tangente in un punto della curva tramite le derivate
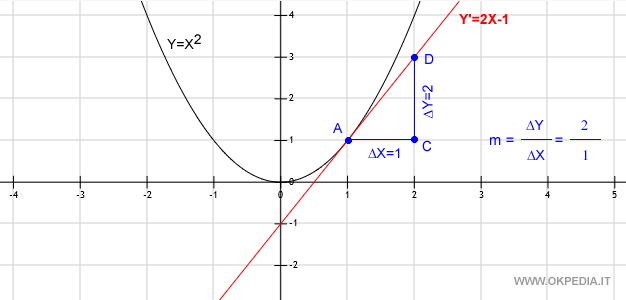
Data una funzione y=x2, la sua rappresentazione grafica sul diagramma cartesiano è una parabola che passa per l'origine.
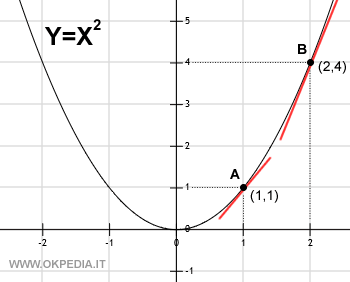
Come si può notare, la curva ha un'inclinazione diversa in ogni suo punto. Pertanto, il coefficiente angolare della tangente cambia in ogni punto della curva.
Esempio. I punti A e B della curva hanno una retta tangente con un coefficiente angolare differente. L'inclinazione della retta tangente è diversa.
Per trovare la retta tangente in un qualsiasi punto della curva, si utilizzano due concetti.
- La derivata della funzione. In questo caso la derivata della funzione x2 è 2x.
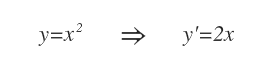
- L'equazione della retta generica. Una qualsiasi retta può essere scritta tramite l'equazione (y-y0)=m(x-x0) dove m è il coefficiente angolare mentre (x0,y0) è un punto qualsiasi della retta.
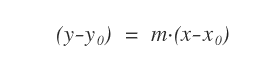
Esempio 1
Il punto B si trova alle coordinate ( 2, 4 ) ossia x0=2 e y0=4,

La derivata della funzione permette di trovare il coefficiente angolare (m) della retta tangente in B.
La derivata di x2 è 2x.
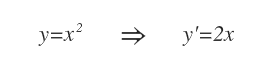
Considerando che X0=2 nel punto B, il coefficiente angolare è quattro.
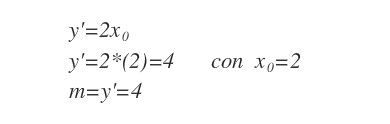
Ora si sostituisce m=4, X0=2 e Y0=4 nell'equazione della retta generica.
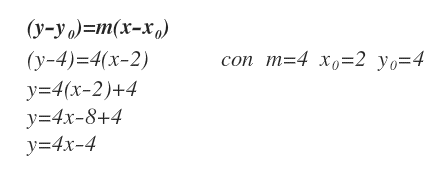
Si ottiene così l'equazione della retta tangente nel punto B della curva alle coordinate (2,4) ossia y=4x-4.
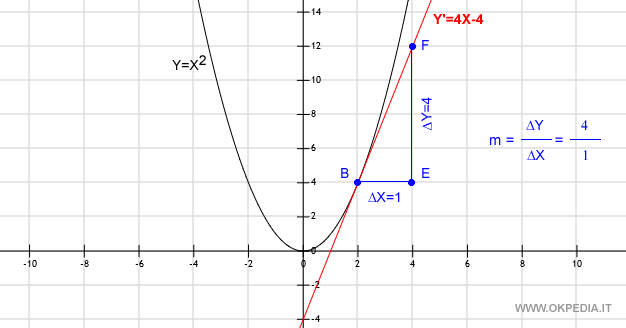
Lo stesso procedimento può essere utilizzato per costruire la retta tangente in qualsiasi altro punto della funzione.
Esempio 2
Il punto A si trova alle coordinate ( 1, 1 ) ossia x0=1 e y0=1,

Per trovare il coefficiente angolare (m) della retta tangente in A si sostituisce X0=1 nella derivata della funzione (y'=2x).
In questo caso il coefficiente angolare della retta tangente è uguale a due (m=2).
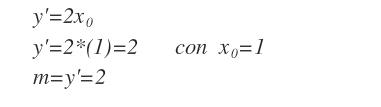
A questo punto si sostituisce m=2, X0=1 e Y0=1 nell'equazione della retta generica.
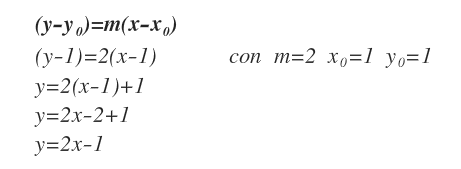
Si ottiene così la retta tangente nel punto A ossia Y = 2X-1.
Lo stesso procedimento può essere usato per calcolare l'equazione della retta tangente in qualsiasi altro punto della funzione. Ad esempio, per trovare l'equazione della retta tangente nel punto P(4,16) il calcolo è il seguente: