Regola di De L'Hôpital
La regola o teorema di De L'Hôpital è un procedimento dell'analisi matematica che consente di calcolare il limite di una funzione in un punto di indecisione 0/0 oppure ∞/∞.
Il limite del rapporto di due funzioni in un punto di indecisione 0/0 oppure ∞/∞, è uguale, se esiste, al limite del rapporto delle loro derivate.
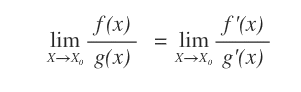
Cos'è un punto di indecisione? Una forma di indecisione è un punto in cui il rapporto tra due funzioni f(x)/g(x) è indeterminato perché è uguale a 0/0 oppure ∞/∞. In questi punti di indecisione non è calcolabile il quoziente delle funzioni reali.
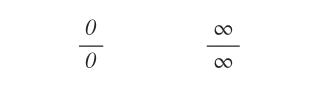
Un esempio pratico sul teorema di De L'Hôpital
La seguente funzione assume la forma indeterminata 0/0 quando x = 2.
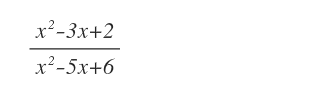
E' una delle forme indeterminate in cui si può usare il teorema di De L'Hôpital.
Si calcola separatamente la derivata del numeratore e del denominatore.
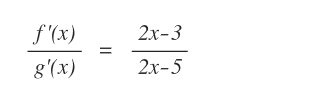
Nota. Per attuare il teorema di De L'Hôpital non bisogna calcolare la derivata del rapporto come avviene nel calcolo differenziale bensì delle singole funzioni al numeratore e al denominatore.
A questo punto si calcola il limite del rapporto delle derivate intorno al punto di indeterminazione x=2.
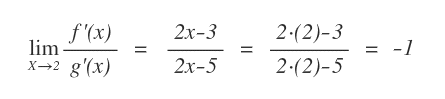
Secondo il teorema di De L'Hôpital anche il limite del rapporto f(x)/g(x) in x=2 è uguale a -1
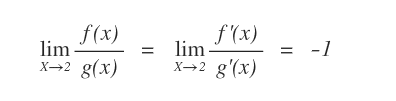
In questo modo, grazie alla regola di De L'Hôpital si trova il limite della funzione nel punto in cui è indeterminata.
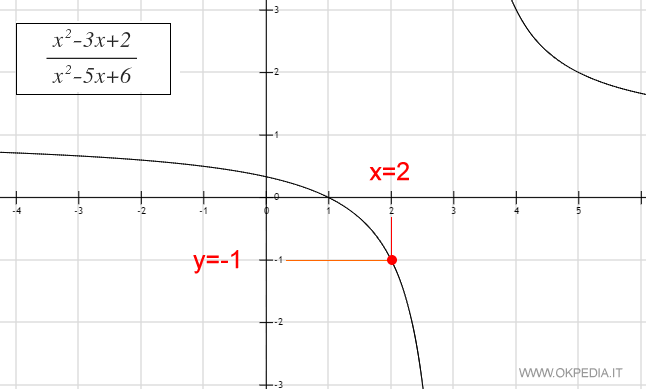
Verifica. Per verificare il risultato appena trovato con la regola di De L'Hopital costruiamo il grafico della funzione f(x). Nel punto x=2 la funzione assume il valore f(x)=-1. Pertanto, il risultato è corretto.