A cosa serve la derivata
Lo studio della derivata di una funzione nasce inizialmente per risolvere problemi geometrici, ossia per trovare l'inclinazione della retta tangente in un punto di una curva. Tuttavia, le applicazioni sono molteplici.
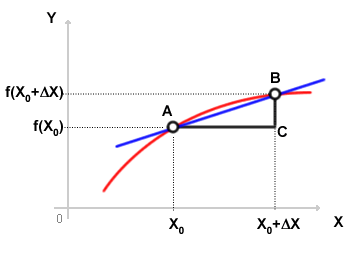
Oggi le derivate sono utilizzate praticamente in discipline di ogni campo del sapere, come strumento di indagine per studiare le caratteristiche delle funzioni.
Quali informazioni si ottengono dalla derivata di una funzione?
Lo studio della derivata di una funzione consente di trovare le seguenti informazioni sulla funzione:
- crescenza
- decrescenza
- concavità
- convessità
- asintoti
- flessi ( crescenti o decrescenti )
- punti di massimo
- punti di minimo
Esempio. Il calcolo della derivata di una funzione è usato in fisica per calcolare l'accelerazione istantanea di un corpo, in economia per studiare il prodotto marginale di una funzione di produzione, in statistica per calcolare il tasso di crescita demografico di una popolazione e così via.
Un esempio pratico di derivata
Un'automobile percorre 100 km in un'ora dal punto A al punto B.

E' quindi possibile affermare che la velocità media del veicolo è pari a 100 km ogni 60 minuti.

Tuttavia, durante il tragitto il veicolo ha cambiato più volte la velocità. A volte ha rallentato, altre volte ha accelerato.
Dalla velocità media non possiamo capire se il veicolo sta accelerando o rallentando in un particolare istante t1.
Per conoscere l'accelerazione del veicolo nell'istante t1 si ricorre alla derivata prima della funzione del moto V(t).
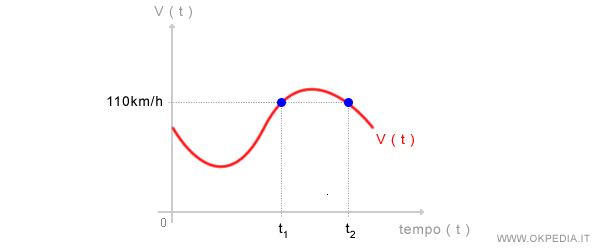
Nella funzione del moto V(t) sono registrate tutte le velocità istantanee del veicolo nel tempo, minuto dopo minuto.
Un esempio di accelerazione
La derivata prima della funzione V(t) permette di capire se il veicolo sta accelerando o decelerando in quel preciso momento.
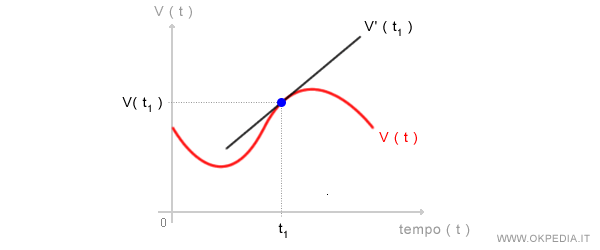
In questo caso, nell'istante t1 la funzione derivata V' ha un'inclinazione positiva ossia sta crescendo.
Questo ci permette di capire che in quel momento il veicolo sta accelerando.
Un esempio di decelerazione
Nell'istante t2 la funzione derivata V' è inclinata negativamente. Il coefficiente angolare è negativo.
In quest'altro caso si deduce che il veicolo sta decelerando.
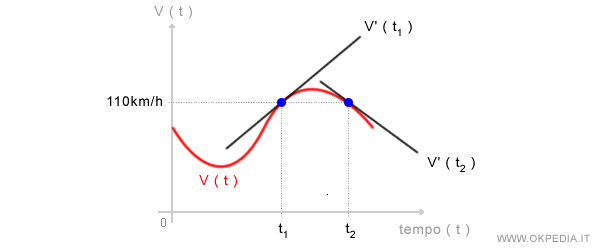
Sia nell'istante t1 che t2 il veicolo ha la stessa velocità istantanea ( 110 km/h ).
Grazie alla derivata prima della funzione V(t) è possibile capire che nell'istante t1 il veicolo sta accelerando mentre nell'istante t2 sta rallentando.
