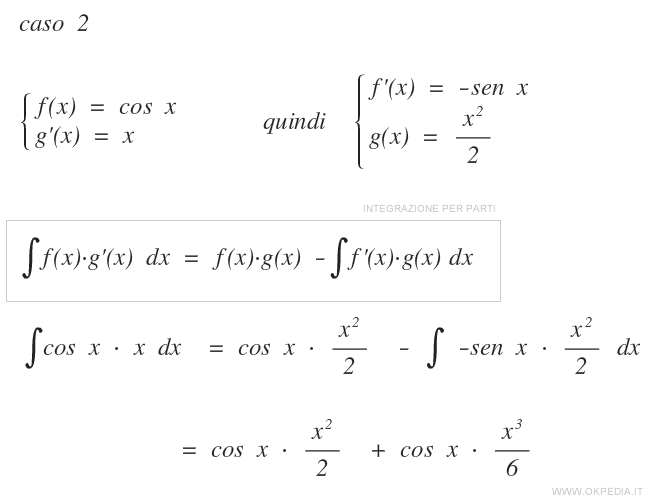Integrazione per parti
Nel calcolo infinitesimale l'integrazione per parti è un metodo di risoluzione degli integrali.
La formula dell'integrazione per parti
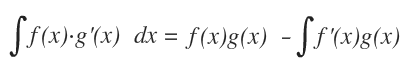
Date due funzioni f(x) e g(x) con derivata continua in un intervallo [a,b], l'integrale è risolvibile con la formula dell'integrazione per parti.
E' un metodo di risoluzione e di calcolo degli integrali, insieme all'integrazione per sostituzione.
La spiegazione dell'integrazione per parti
La formula si applica soltanto quando la funzione integranda è il prodotto di due fattori: f(x) e g'(x)dx

- f(x) è detto fattore finito
- g'(x)dx è detto fattore differenziale
La scelta del fattore finito e differenziale dipende dalla convenienza del calcolo.
Nota. Il fattore finito va derivato mentre il fattore differenziale va integrato. A seconda della complessità del calcolo, si sceglie la via più semplice per la derivazione e l'integrazione.
La dimostrazione dell'integrazione per parti
Date due funzioni f(x) e g(x) continue e derivabili in un intervallo [a,b], la derivata del loro prodotto F[f(x)·g(x)] è uguale a f'(x)·g(x)+f(x)·g'(x).
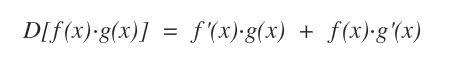
Integriamo entrambi le parti
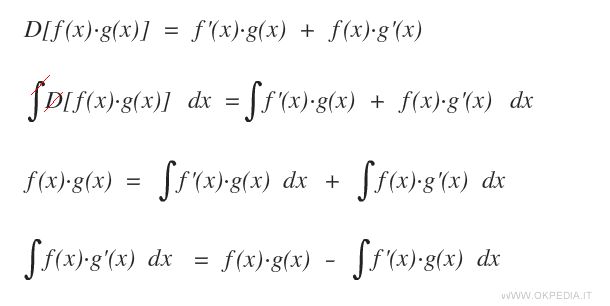
Ora isoliamo l'integrale f(x)g'(x)dx a sinistra e otteniamo la formula dell'integrazione per parti.
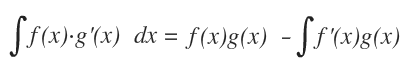
Questi passaggi dimostrano la formula dell'integrazione per parti a partire dalla regola di derivazione del prodotto di due funzioni.
Un esempio di calcolo dell'integrale
Per calcolare l'integrale utilizziamo la formula dell'integrazione per parti.

La soluzione dell'integrale è x·sen x + cos x.
Nota. Per calcolare l'integrale potremmo scegliere anche la strada alternativa ma la procedura di calcolo sarebbe molto più complessa. Per questa ragione, nell'integrazione per parti la scelta del fattore finito e differenziale è una scelta puramente di convenienza di calcolo.