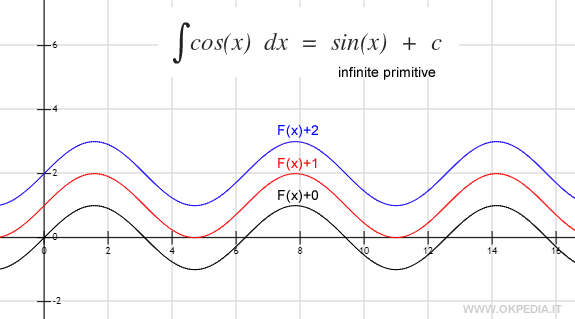
Integrale indefinito
L'integrale indefinito di una funzione f(x) è l'insieme di tutte le funzioni primitive F(x)+c di f(x), dove c è un numero reale qualsiasi. L'integrale indefinito è indicato con il simbolo ∫.

La parte ∫f(x)dx è detta funzione integranda mentre la variabile x è detta variabile di integrazione.
Nota. Nella pratica il simbolo dell'integrale indefinito può essere usato sia per indicare l'insieme di tutte le funzioni primitive F(x)+c, sia una qualsiasi funzione primitiva F(X).
Le funzioni f(x) che ammettono una primitiva F(x) sono dette funzioni integrabili.
Un esempio di integrale indefinito
Data la funzione f(x)=2x
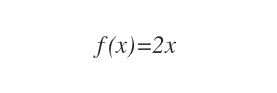
l'integrale indefinito di f(x) indica tutte le funzioni primitive F(x) la cui derivata è uguale a f(x).
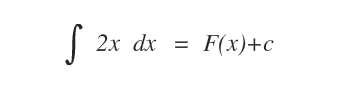
Ad esempio, le seguenti funzioni primitive hanno la derivata uguale a f(x)

Per questa ragione la famiglia delle primitive è indicata nella forma F(x)+c.
In questo caso, l'integrale indefinito di f(x)=2x è la famiglia di funzioni primitive x2+c.
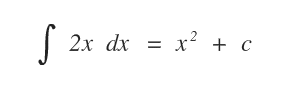
A cosa serve la costante c dell'integrale
La costante reale c è un numero qualsiasi, perché la derivata di una costante è comunque uguale a zero D[c]=0.
Esempio
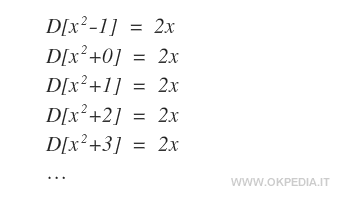
Il simbolo della costante c nell'integrale indefinito indica l'infinito numero di primitive F(x) della funzione f(x).
In conclusione, se una funzione f(x) è integrabile ammette un infinito numero di primitive F(x) che differiscono tra loro per un valore costante c.
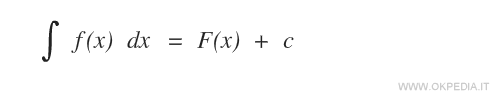
Per questa ragione è sufficiente calcolare una sola primitiva fondamentale F(x) della funzione.
La primitiva fondamentale è la primitiva F(x) che si ottiene con c=0.

Nota. Le altre funzioni primitive si possono comunque aggiungendo semplicemente una qualsiasi costante c alla F(x). Ad esempio, l'integrale della funzione f(x)=cos(x) è F(X)=sin(x)+c perché la derivata di qualsiasi primitiva D[sin(x)+c] è uguale a cos(x).