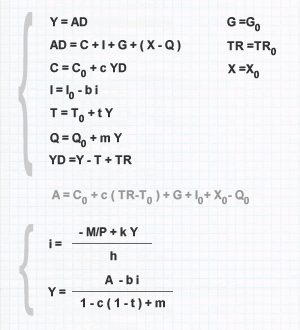Funzione degli investimenti
La funzione degli investimenti è la relazione economica tra la quantità degli investimenti e il tasso di interesse di mercato. È utilizzata nel modello IS-LM. Tra investimenti e tasso di interesse sussiste una relazione inversa. Un aumento del tasso di interesse provoca un aumento del prezzo del denaro. A parità di condizioni, per accedere a un finanziamento gli investitori devono riconoscere più interessi al creditore. Ciò determina una riduzione della quantità degli investimenti da parte dell'impresa ( spesa per investimenti ). Viceversa, una riduzione del tasso di interesse produce l'effetto inverso, si riduce il costo del denaro e l'impresa può accedere al finanziamento con minore onere sugli interessi. Questo spinge l'imprenditore ad aumentare la spesa per investimenti. Nel modello IS-LM la funzione degli investimenti può essere scritta nel seguente modo:
I = I0 - b·i
La spesa per investimenti ( I ) è determinata nel seguente modo. A partire dal valore degli investimenti I0 che si avrebbe se il tasso di interesse fosse nullo ossia pari a zero ( i = 0 ), si detrae il tasso di interesse corrente ( i ) moltiplicato per la sensibilità ( b ) alle variazioni del tasso di interesse degli operatori economici ( b > 0 ). Ad esempio, in assenza di sensibilità alle variazioni del tasso di interesse ( b = 0 ) la spesa per investimenti è indipendente dalle variazioni del tasso di interesse. Viceversa, quando la variabile ( b ) ha valori molto alti, la spesa degli investimenti è fortemente dipendente dalle variazioni del tasso di interesse. La funzione degli investimenti può essere rappresentata su un diagramma cartesiano, ponendo il valore degli investimenti sull'asse delle ascisse e il tasso di interesse sull'asse delle ordinate.
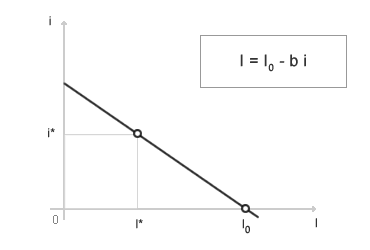
Sul piano cartesiano la funzione degli investimenti ha un andamento decrescente. Un aumento del tasso di interesse ( i ) riduce la spesa degli investimenti ( I ) delle imprese, e viceversa. Il punto di intercetta I0 sull'asse dell'ascisse indica il valore degli investimenti se il tasso di interesse fosse nullo ( i = 0 ). Ad esempio, il tasso di interesse i* determina una spesa per investimenti I*. La rappresentazione grafica consente anche di analizzare meglio la sensibilità ( b ) alle variazioni del tasso di interesse. Nel seguente diagramma sono rappresentati due casi opposti:
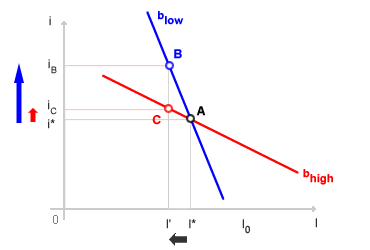
Nella funzione di investimento con elevata sensibilità ( bhigh ), una minima variazione del tasso di interesse determina una elevata variazione della spesa per investimenti ( I ). La funzione degli investimenti appare quasi piatta. Nella funzione di investimento con bassa sensibilità ( blow ), invece, la variazione del tasso di interesse produce una minima variazione della spesa per investimenti. La domanda degli investimenti è rigida. Ad esempio, si supponga di voler ridurre gli investimenti da I* a I'. Nella funzione degli investimenti più sensibile ( bhigh ) è sufficiente una piccola variazione del tasso di interesse da i* a iC. L'equilibrio si sposta da A a C. Nella funzione degli investimenti meno sensibile ( blow ) è, invece, necessaria una grande variazione del tasso di interesse da i* a iB poiché le decisioni di investimento delle imprese sono meno dipendenti dal livello del tasso di interesse. Il punto di equilibrio si sposta da A a B.
Dal modello reddito-spesa al modello IS-LM. Nel modello reddito-spesa il livello degli investimenti è considerato costante ( variabile esogena ) e determinato dalle aspettative di lungo periodo delle imprese. L'introduzione della funzione degli investimenti nel modello reddito-spesa consente di collegare il tasso di interesse alle variazioni della domanda aggregata ( AD ) e del reddito ( Y ) tramite le variazioni indotte sulla spesa per investimenti ( I ).
Poiché il tasso di interesse ( i ) è anche una variabile determinante nel mercato monetario, ciò consente di individuare il livello del tasso di interesse ( i* ) tale da porre in equilibrio contemporaneamente sia il mercato reale degli investimenti/risparmio ( scheda IS ) e sia il mercato monetario ( scheda LM ). L'introduzione della funzione degli interessi consente di passare dal modello reddito-spesa al modello IS-LM.
