Ricerca locale proposizionale
La ricerca locale proposizionale è un algoritmo di ricerca delle soluzioni applicato al calcolo proposizionale. Data una formula logica, l'algoritmo seleziona una componente logica interna ( clausola ) per analizzarne le condizioni di soddisfacibilità logica locale della clausola. Dopo aver soddisfatto la singola clausola locale, ne seleziona un'altra tra quelle non ancora soddisfatte, fino a giungere alla soluzione o a un insieme vuoto ( assenza soluzione ). Il processo di ricerca si ripete ciclicamente N volte a partire da clausole iniziali diverse. La selezione delle clausole può essere basata su una scelta casuale ( random ) oppure su apposite euristiche di scelta. Ad esempio, la seguente formula logica è composta da tre clausole.
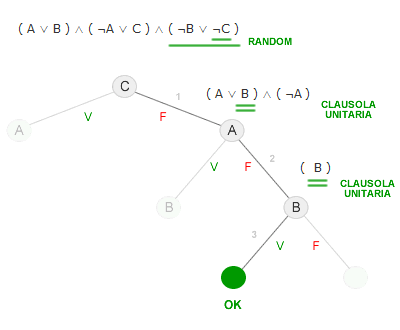
- Prima selezione ( casuale ). La prima selezione è casuale ( random ). L'algoritmo sceglie casualmente la clausola iniziale da soddisfare. Nell'esempio precedente l'algoritmo seleziona la clausola ( ¬B ∨ ¬C ). Una volta scelta la clausola iniziale, l'algoritmo seleziona casualmente un letterale e gli attribuisce il valore di verità, ossia il valore booleano tale da rendere vera la clausola. Nell'esempio precedente l'algoritmo seleziona casualmente il letterale C e gli assegna il valore "false", in modo tale da rendere vera la clausola. Da sottolineare un aspetto importante, il valore logico assegnato al letterale (C) viene applicato su tutta la formula e non soltanto sulla clausola locale. Dopo l'assegnazione del valore "false" alla variabile C, l'algoritmo aggiorna l'intera formula logica, eliminando le clausole vere e i letterali falsi.
- Seconda selezione ( euristica ). La seconda selezione può essere casuale o informata. Nell'esempio abbiamo optato per una selezione euristica poiché la formula logica è caratterizzata da una clausola unitaria (¬A). È razionale che l'algoritmo selezioni subito la clausola unitaria, poiché da quest'ultima dipende la soddisfacibilità o meno della formula logica. Nell'esempio precedente l'algoritmo assegna il valore "false" al letterale A, rendendo vera la seconda clausola, e aggiorna la formula logica.
- Terza selezione ( euristica ). Nella terza e ultima selezione la formula logica è composta soltanto dal letterale (B) ed è, pertanto, una clausola unitaria. È sufficiente trovare il valore di verità di quest'ultima (B=true) per trovare la soluzione dell'intera formula logica.
Nei vari passaggi l'algoritmo utilizza la selezione casuale ( prima selezione ), la selezione informata ( seconda selezione ) e la selezione unica ( terza selezione ). La scelta casuale consente di esplorare l'albero logico senza considerare un particolare ordine di assegnamento delle variabili.
- Soluzione trovata. Quando l'algoritmo trova la prima soluzione valida la restituisce in output, dimostrando indirettamente anche la soddisfacibilità della stessa. L'esecuzione può essere interrotta. L'algoritmo può anche memorizzare la soluzione e iniziare un'altra elaborazione alla ricerca di altre soluzioni migliori.
- Soluzione non trovata. Quando l'algoritmo non trova una soluzione ( es. contraddizione logica ), evita il punto di minimo locale interrompendo l'esplorazione e inizia un nuovo ciclo di esplorazione scegliendo casualmente un'altra clausola iniziale.
Dopo n cicli l'elaborazione viene interrotta. Quanto maggiore è il numero di tentativi massimi (n) o cicli di elaborazione, tanto maggiore è la probabilità che l'algoritmo giunga a una soluzione.
 Selezione casuale. La selezione casuale della clausola e del letterale è particolarmente utile nei casi in cui non è possibile elaborare le euristiche. Ad esempio, l'elaborazione dinamica delle euristiche potrebbe consumare una grande quantità di risorse di memoria e di tempo di elaborazione. In tali casi la selezione casuale potrebbe agevolare l'esplorazione delle combinazioni possibili senza seguire un ordine prestabilito di assegnazione dei valori alle variabili.
Selezione casuale. La selezione casuale della clausola e del letterale è particolarmente utile nei casi in cui non è possibile elaborare le euristiche. Ad esempio, l'elaborazione dinamica delle euristiche potrebbe consumare una grande quantità di risorse di memoria e di tempo di elaborazione. In tali casi la selezione casuale potrebbe agevolare l'esplorazione delle combinazioni possibili senza seguire un ordine prestabilito di assegnazione dei valori alle variabili.
 Non completezza. L'algoritmo di ricerca locale proposizionale non è completo, in quanto non esplora l'intero albero logico del problema. Quando giunge a una soluzione, o a più soluzioni, non è detto che siano le migliori soluzioni possibili.
Non completezza. L'algoritmo di ricerca locale proposizionale non è completo, in quanto non esplora l'intero albero logico del problema. Quando giunge a una soluzione, o a più soluzioni, non è detto che siano le migliori soluzioni possibili.
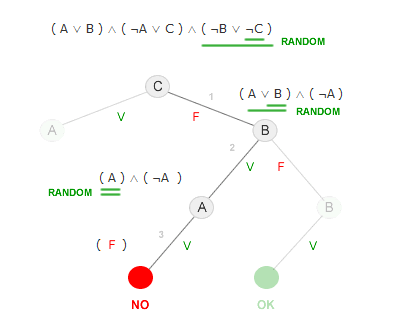
- Euristiche dinamiche. È consigliabile integrare alcune euristiche nell'algoritmo di ricerca. Senza appesantire eccessivamente l'elaborazione, integrare qualche euristica fondamentale consente di migliorare l'efficienza della scelta casuale. Ad esempio, se l'algoritmo si trova dinnanzi a una clausola unitaria, è opportuno selezionarla prima delle altre. Nel seguente ciclo di ricerca, al secondo passo l'algoritmo seleziona casualmente il letterale B anziché la clausola unitaria (¬A). In questo caso la scelta è fallimentare poiché conduce a una contraddizione ( A ∨ ¬A ). La scelta della clausola unitaria è un'euristica fondamentale e prioritaria poiché, in tutti i casi, senza soddisfare la clausola unitaria anche la formula logica non può essere soddisfata.
- Walksat. L'algoritmo Walksat è un esempio di algoritmo di ricerca locale applicato al calcolo proposizionale. L'algoritmo alterna la selezione casuale e una selezione euristica. La regola della selezione euristica è molto semplice, una volta selezionata la clausola logica in modo casuale, l'algoritmo sceglie il letterale in grado di soddisfare il maggior numero di clausole della formula logica. Per evitare i punti di minimo locale l'algoritmo alterna una fase di selezione euristica del letterale a una fase di selezione casuale, in modo tale da coniugare i vantaggi dell'esplorazione casuale con quelli di una selezione intelligente ( euristica ).
- Insoddisfacibilità logica.Se dopo n tentativi l'algoritmo di ricerca locale non trova una soluzione valida al problema, interrompe l'esecuzione e restituisce il fallimento. Il fallimento non dimostra l'insoddisfacibilità della formula logica, in quanto l'algoritmo non è completo. Tuttavia, dopo n tentativi l'algoritmo può fornire una stima probabilistica sull'esistenza o meno di una soluzione ( soddisfacibilità logica ).
- Problemi sottovincolati. La ricerca locale proposizionale è un metodo efficiente per verificare la soddisfacibilità logica dei problemi sottovincolati. Un problema è detto sottovincolato quando il rapporto tra il numero delle clausole e il numero delle variabili è molto basso. In questi casi, il numero dei vincoli tra le variabili è ridotto e l'algoritmo può verificare o meno la soddisfacibilità SAT dopo pochi tentativi.
