Algoritmo DPLL
L'algoritmo DPLL è un algoritmo di verifica della soddisfacibilità booleana della logica proposizionale di primo ordine e di risoluzione di un problema SAT tramite la tecnica del backtracking. L'algoritmo consente di verificare la soddisfacibilità delle formule espresse nella forma normale congiuntiva ( CNF ) ossia di verificare se una determinata formula è vera o falsa. Nell'algoritmo DPLL le variabili ( letterali ) della formula logica sono selezionate iterativamente, risolvendo ogni clausola in cui compare la variabile ( letterale ) in questione con quelle in cui compare la negazione della variabile. L'algoritmo DPLL riesce a determinare se una formula è soddisfacibile o meno, tramite un processo di analisi incompleto ma efficace. Ad esempio, la seguente formula proposizionale è composta da tre clausole in forma congiuntiva.

Una clausola è vera se i letterali che la compongono sono veri, fatta eccezione per quelli a cui non è stato assegnato un valore. Viceversa, una clausola è falsa se i letterali che la compongono sono falsi. Quando una qualsiasi delle clausole è falsa, anche la formula è falsa. In questi casi l'algoritmo può terminare l'enumerazione del model checking corrente per fare un passo indietro ( backtracking ) e analizzare il modello successivo. Ciò consente di realizzare la potatura logica dell'albero logico durante l'elaborazione, risparmiando tempo e risorse.

Quando una clausola ha un letterale positivo è inutile indagare sugli altri letterali poiché qualsiasi valore abbiano gli altri letterali lo stato della clausola è sempre vero ( true ). È preferibile continuare l'enuemerazione sui letterali non assegnati delle clausole non ancora vere. Ad esempio, se il letterale A è falso ( false ), le prime due clausole sono vere indipendentemente dagli altri letterali. L'algoritmo può concentrare l'elaborazione sui letterali della terza clausola.

Questa caratteristica dell'algoritmo può far risparmiare notevoli risorse e tempo di elaborazione. La potatura logica dell'albero logico è determinata dall'ordine di assegnazione dei letterali. Ad esempio, assegnando il valore vero ( true ) al letterale B come prima istanza, l'algoritmo elimina la prima e la terza clausola, potendo così dedicarsi soltanto ai letterali non assegnati della seconda clausola ( A e C ). In tal modo l'algoritmo evita l'assegnazione sul letterale D, presente soltanto nella terza clausola, poiché quest'ultima è già vera.
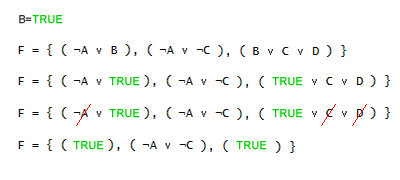
Il processo model checking si interrompe quando almeno una clausola ha tutti i letterali falsi, in quanto se una clausola è falsa allora anche la formula è falsa, per passare all'analisi del modello successivo tramite la tecnica della ricerca backtracking in profondità. Ad esempio, assegnando il valore vero ( true ) al letterale A e il valore falso ( false ) al letterale B, la prima clausola assume tutti valori negativi ed è, pertanto, falsa ( insoddisfacibile ). Se la prima clausola è falsa anche la formula è falsa, indipendentemente dai valori non ancora assegnati ( C, D ) delle altre clausole. L'algoritmo può interrompere la ricerca in profondità e passare al modello successivo.

Viceversa, quando tutte le clausole sono vere anche la formula è vera ( soddisfacibilità SAT ). Anche in questo caso, dopo aver individuato una situazione di soddisfacibilità SAT, l'algoritmo procede con l'elaborazione del modello successivo mediante la tecnica del backtracking. Ad esempio, quando l'algoritmo assegna il valore vero ( true ) al letterale B e il valore falso ( false ) al letterale C, tutte le clausole sono vere e, indipendentemente dall'assegnazione dei letterali A e D, anche la formula logica è vera, quindi è soddisfacibile.

 Efficienza. L'algoritmo DPLL è particolarmente efficiente in quanto riesce a valutare se una formula è vera o falsa senza dover analizzare tutti i modelli possibili ( model checking ) e senza penalizzare la completezza dell'analisi. Quando l'algoritmo rileva una clausola falsa interrompe l'analisi del model checking su quel modello ( terminazione anticipata ) e compie un passo indietro ( backtracking ) per analizzare la successiva assegnazione di valori ( modello successivo ).
Efficienza. L'algoritmo DPLL è particolarmente efficiente in quanto riesce a valutare se una formula è vera o falsa senza dover analizzare tutti i modelli possibili ( model checking ) e senza penalizzare la completezza dell'analisi. Quando l'algoritmo rileva una clausola falsa interrompe l'analisi del model checking su quel modello ( terminazione anticipata ) e compie un passo indietro ( backtracking ) per analizzare la successiva assegnazione di valori ( modello successivo ).
 Algoritmo Davis-Putnam (DP). Il nome DPLL deriva dalle iniziale degli autori che, negli anni '60, contribuiscono alla sua stesura: Martin Davis, Hilary Putnam, George Logemann e Donald W. Loveland. È anche conosciuto come algoritmo di Davis-Putnam, algoritmo DP o algoritmo DPL. Va comunque sottolineato che l'algoritmo Davis-Putnam (DP) e l'algoritmo DPLL sono due algoritmi distinti, seppure correlati, ed è scorretto riferirsi a entrambi con la medesima nomenclatura DPLL. L'algoritmo DPLL utilizza il criterio splitting rule anziché applicare il metodo della risoluzione dell'algoritmo Davis-Putnam. L'algoritmo Davis-Putnam viene ideato nel 1960 mentre l'algoritmo DPLL nel 1962.
Algoritmo Davis-Putnam (DP). Il nome DPLL deriva dalle iniziale degli autori che, negli anni '60, contribuiscono alla sua stesura: Martin Davis, Hilary Putnam, George Logemann e Donald W. Loveland. È anche conosciuto come algoritmo di Davis-Putnam, algoritmo DP o algoritmo DPL. Va comunque sottolineato che l'algoritmo Davis-Putnam (DP) e l'algoritmo DPLL sono due algoritmi distinti, seppure correlati, ed è scorretto riferirsi a entrambi con la medesima nomenclatura DPLL. L'algoritmo DPLL utilizza il criterio splitting rule anziché applicare il metodo della risoluzione dell'algoritmo Davis-Putnam. L'algoritmo Davis-Putnam viene ideato nel 1960 mentre l'algoritmo DPLL nel 1962.
- Splitting rule. L'algoritmo DPLL utilizza il criterio splitting rule anziché applicare il metodo della risoluzione dell'algoritmo Davis-Putnam. Il criterio dello splitting rule si basa su una procedura di branching in cui un letterale ( variabile ) viene inizialmente assegnato nei due valori booleani ( vero o falso ) per proseguire alla ricerca della soluzione in profondità mediante l'analisi in profondità degli altri letterali. Quando un modello non consente di raggiungere una soluzione, l'algoritmo effettua un passo indietro ( backtracking ) sulla ramificazione per analizzare le assegnazioni alternative.
- Terminazione anticipata. La terminazione anticipata attua una potatura logica sia del modello in questione che delle sottoramificazioni possibili, ottenendo quindi un taglio su diversi modelli e non su uno solo. La terminazione anticipata si verifica in due casi:
- Se tutte le clausole sono vere anche la formula è vera. In questi casi è inutile analizzare i valori delle altre variabili ( letterali ) non ancora assegnate. L'algoritmo può terminare l'elaborazione del modello e passare all'analisi del modello successivo. Ad esempio, data una formula ( A ∨ B ) ∧ ( A ∨ C ). Se il letterale A è vero, le due clausole sono vere e, pertanto, anche la formula è vera. In questo caso è inutile analizzare i valori booleani dei letterali B e C poiché non aggiungerebbero alcuna informazione rilevante. In modo simile, la terminazione anticipata si applica quando una clausola è falsa.
- Se una clausola è falsa anche la formula è falsa ed è, quindi, inutile analizzare le clausole restanti del modello. Ad esempio, data la formula ( A ) ∧ ( B ∨ C ), se il letterale A è falso lo è anche la formula logica, indipendentemente dai valori assegnabili ai letterali B e C.
- Backtracking. La funzione backtracking consente di tornare alla combinazione dei valori precedente alla situazione critica. Nell'algoritmo DPLL la funzione backtracking viene richiamata ogni volta che si presenta una terminazione anticipata.
- Euristiche. L'efficienza dell'algoritmo DPLL può essere ulteriormente migliorata tramite l'utilizzo delle euristiche. Le euristiche più note sono le seguenti:
- Euristica del simbolo puro. Un simbolo puro è un letterale che compare nelle clausole sempre nella stessa forma, positiva o negativa. Ad esempio, nella formula il letterale A è un simbolo puro poiché compare sempre nella stessa forma positiva.
( A ∨ B ) ∧ ( A ∨ C ) ∧ ( ¬B ∨ ¬C )
In questo caso è consigliabile elaborare prima i simboli puri per ottenere una potatura logica più efficace e per concentrare il resto dell'elaborazione alle clausole restanti. Assegnando il valore vero ( true ) al letterale A la formula si riduce alla sola clausola residuale ( ¬B ∨ ¬C ). È quindi più semplice valutare la soddisfacibilità della formula e la ricerca delle sue soluzioni. - Euristica della clausola unitaria. Una clausola unitaria è una clausola composta da un unico letterale. Le clausole unitaria devono essere analizzate prima delle altre, in quanto ciò consente di effettuare una potatura logica più marcata dell'albero logico. Ad esempio, nella seguente formula è presente una clausola unitaria ( C ):
( A ∨ B ) ∧ ( C ) ∧ ( ¬B ∨ ¬C )
Per risolvere la formula in modo positivo è necessario assegnare al letterale C il valore di verità "true", tale da rendere vera la clausola. Sarebbe inutile analizzare i valori "false" del letterale C. L'euristica della clausola unitaria consente di semplificare la formula residuale nella seguente forma: ( A ∨ B ) ∧ ( ¬B ). - Euristica della scomposizione. Quando una clausola è composta da un letterale non in comune con le altre clausole, è sufficiente cercare il valore booleano di verità del letterale specifico per rendere vera la clausola ed eliminarla dalla formula. Ad esempio, nella seguente formula logica la terza clausola è caratterizzata da un letterale specifico ( D ).
( A ∨ B ) ∧ ( ¬B ∨ C ) ∧ ( ¬A ∨ ¬C ∨ D )
Scomponendo la clausola di due sottoinsiemi disgiunti, è possibile mettere in evidenza il letterale non in compone, al fine di poterlo trattare la clausola come una clausola unitaria. Una volta assegnato il valore "true" al letterale D, l'intera clausola può essere eliminata dalla formula. - Euristica di grado. L'euristica di grado determina l'ordine di assegnazione delle variabili e dei valori. Secondo l'euristica le variabili con maggiori vincoli con le altre devono essere elaborate prima. In una formula logica ciò equivale a dire che il letterale più comune tra le clausole deve essere elaborato prima nelle operazioni di assegnazioni. Ad esempio, la seguente formula è composta da tre clausole e da quattro variabili.
( A ∨ B ) ∧ ( ¬B ∨ C ) ∧ ( ¬B ∨ ¬C ∨ D )
La variabile B è presente tre volte, di cui due in forma negata (¬B), la variabile C due volte e le restanti variabili A e ¬D una volta. L'ordine di assegnazione migliore è, pertanto, il seguente: ¬B, C, A, ¬D. È molto importante considerare la forma booleana ( normale o negata ) più frequente per ciascuna variabile nell'ordine di assegnamento. - Euristiche dinamiche. Le euristiche di un algoritmo DPLL devono essere elaborate ricorsivamente, ogni qualvolta che la formula logica viene modificata. Durante l'elaborazione dei vari modelli ( model checking ) e l'assegnamento dei valori alle variabili, le clausole della formula logica originaria sono modificate o annullate. E', quindi, possibile che sorgano situazioni intermedie in cui le euristiche possono essere efficacemente applicate. Ad esempio, nella seguente formula non è applicabile nessuna euristica.
( A ∨ B ) ∧ ( ¬A ∨ C ) ∧ ( ¬B ∨ ¬C )
Tuttavia, dopo aver assegnato il valore true al letterale A, è possibile eliminare la prima clausola ( true B ) e il primo letterale ¬A della seconda clausola. La formula logica intermedia è ( C ) ∧ ( ¬B ∨ ¬C ) dove emerge chiaramente una clausola unitaria (C). È quindi consigliabile non limitare l'applicazione delle euristiche soltanto nella fase preliminare dell'elaborazione, quella che precede l'esecuzione vera e propria dell'algoritmo, ma eseguirle ricorsivamente ogni qualvolta la formula logica viene modificata durante l'elaborazione.
- Euristica del simbolo puro. Un simbolo puro è un letterale che compare nelle clausole sempre nella stessa forma, positiva o negativa. Ad esempio, nella formula il letterale A è un simbolo puro poiché compare sempre nella stessa forma positiva.
