Metodo della risoluzione
Il metodo della risoluzione è un metodo logico per dimostrare l'insoddisfacibilità di un insieme S di clausole logiche. È alla base di una regola di inferenza detta risoluzione proposizionale. Dato un insieme S di clausole in cui ogni clausola è composta da letterali, il metodo della risoluzione consiste nel selezionare due clausole ( clausole di premessa ) aventi un medesimo letterale con polarità opposta ( letterale selezionato per la risoluzione ) ossia due letterali complementari. Due letterali sono complementari quando l'uno è la negazione dell'altro ( es. p e ¬p ).
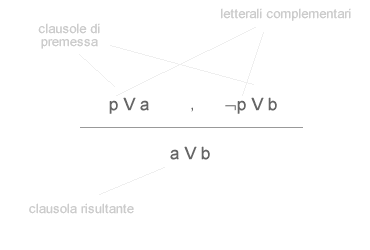
Le due clausole di premessa ( p ∨ a ) e ( ¬p ∨ b ) sono unite tra loro con una disgiunzione (∨) e, una volta annullato il letterale selezionato ( p ∨ ¬p ), danno luogo a una nuova clausola ( a ∨ b ), detta clausola risolvente, che viene a sua volta aggiunta all'insieme iniziale di clausole S. La clausola risolvente è composta da tutti i letterali delle due clausole originali ( premessa ) tranne i due letterali complementari ( opposti ). Il metodo ricomincia un nuovo ciclo mettendo a confronto altre due clausole tratte dall'insieme S. Il processo è detto fattorizzazione e termina quando la risoluzione individua una clausola vuota oppure quando tutte le clausole dell'insieme S sono state analizzate. L'esito del processo della risoluzione è il seguente:
- Insoddisfacibile. L'insieme di clausole S è insoddisfacibile quando la risoluzione individua una clausola vuota. Il processo di risoluzione si interrompe non appena l'algoritmo trova una clausola vuota.
- Soddisfacibile. Tutte le clausole dell'insieme S sono state analizzate e l'insieme S non contiene nessuna clausola vuota. In tale caso l'insieme S è soddisfacibile.
Esempio di applicazione del metodo della risoluzione. Dato un insieme S composto dalle clausole ( A∨¬B∨C ) , ( A∨B ) , ( ¬A∨B ) , ( ¬C ), è possibile applicare il metodo della risoluzione per stabilire se l'insieme S è soddisfacibile o insoddisfacibile. Evitando di analizzare tutte le combinazioni ci si accorge anche a vista d'occhio di una possibile contraddizione. Sono messe a confronto le clausole ( A∨¬B∨C ) e ( ¬A∨B ), le quali hanno ben due letterali complementari.
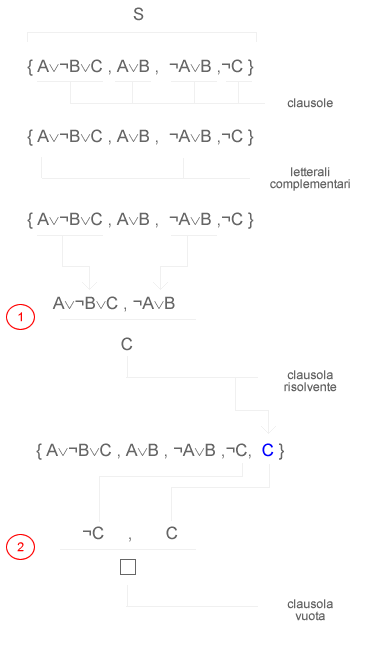
Dalle clausole di premessa ( A∨¬B∨C ) e ( ¬A∨B ) consegue logicamente una clausola risolvente C che viene aggiunta all'insieme delle clausole S. A questo punto la contraddizione è immediatamente visibile, l'insieme S contiene due clausole opposte ( contraddittoria ) ossia C e ¬C. È sufficiente svolgere il secondo ciclo del metodo della risoluzione, mettendo a confronto C e ¬C, per giungere a una clausola vuota come clausola risolvente. È quindi possibile affermare che l'insieme S non è soddisfacibile.

Conseguenza logica. Quando un insieme è insoddisfacibile si verifica una conseguenza logica valida. Ad esempio, data la seguente conseguenza logica proviamo a capire se questa è valida oppure no. Il problema viene trasformato in un problema di soddisfacibilità, trasformando l'ultima formula in una clausola e applicando la risoluzione.
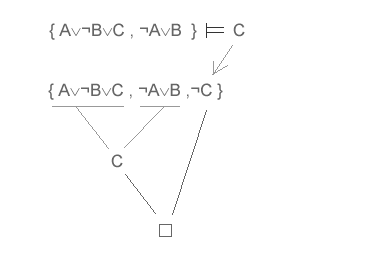
Il processo di risoluzione conduce a una clausola vuota, pertanto l'insieme è insoddisfacibilee la conseguenza logica è valida. La procedura basata sulla risoluzione utilizza il principio della dimostrazione per assurdo. In altri termini per dimostrare una conseguenza logica ( A 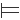 B ) è sufficiente dimostrare che ( A ∧ ¬B ) è insoddisfacibile. Per questa caratteristica il metodo della risoluzione è utilizzato come regola di inferenza logica e negli algoritmi di inferenza per risoluzione.
B ) è sufficiente dimostrare che ( A ∧ ¬B ) è insoddisfacibile. Per questa caratteristica il metodo della risoluzione è utilizzato come regola di inferenza logica e negli algoritmi di inferenza per risoluzione.
- Fattorizzazione. Nella logica proposizionale la fattorizzazione è il processo in cui le coppie di clausole sono confrontate tra loro per produrre una nuova clausola da aggiungere all'insieme del problema..Il processo di fattorizzazione si conclude quando tutte le clausole sono state confrontate oppure quando viene prodotta una clausola vuota.
- Forma normale congiuntiva ( CNF ). Il metodo della risoluzione è utilizzabile soltanto alle clausole ( disgiunzioni di letterali ). Per applicare il metodo anche alle proposizioni logiche ( formule logiche ) è necessario convertire queste ultime in clausole. La rappresentazione delle proposizioni/formule sotto forma di clausole è detta CNF ( Conjunctive Normal Form ) o forma normale congiuntiva.
- Risoluzione del primo ordine. Il metodo della risoluzione è applicabile anche alla logica del primo ordine quando la base di conoscenza delle formule è rappresentata nella forma normale congiuntiva ( CNF ). Il processo di unificazione/sostituzione nella logica del primo ordine è simile a quello della logica proposizionale.
