Calcolo proposizionale ( semantica )
La semantica del calcololo proposizionale consente di definire le regole per attribuire un significato alle formule di un modello. Nella logica proposizionale ogni formula è composta da proposizioni logiche, connettivi logici ( and, or, not, ecc. ) e valori di verità ( vero e falso ). Ad esempio, scrivendo A=>B è possibile se la proposizione logica A è vera allora anche la proposizione logica B è vera. Tuttavia, se la proposizione logica A è falsa non è possibile affermare nulla sulla proposizione logica B.
A⇒B
La semantica del modello consente di associare alle formule, semplici o complesse, un valore di verità e costruire una tavola di verità con tutte le varie combinazioni di stati possibili. Nella logica proposizionale la semantica consiste in una serie di asserzioni che, indipendentemente dal fatto che siano giuste o sbagliate, consentono di attribuire un significato alle formule. Ad esempio, riprendendo l'esempio dell'algoritmo di ricerca inferenziale, un agente razionale si trova alle coordinate (1,1) e non conosce la mappa dell'ambiente in cui si trova. Può soltanto scorgere le informazioni dai quadranti limitrofi.
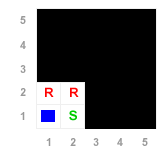
In ogni quadrante l'agente può udire rumore (R) o silenzio (S), oppure scorgere l'obiettivo (O). Nella mappa sono dislocati dei punti di pericolo ( P ) circondati da zone rumorose ( R ). Alle coordinate (1,1) l'agente rileva rumore nel quadrante (1,2), può quindi dedurre che nel quadrante più lontano (1,3) ci sia un'altra zona di rumore ( R ) oppure un punto di pericolo ( P ).
R1,2 ⇒ ( R1,3 ∨ P1,3 )
L'agente rileva rumore anche nella cella limitrofa (2,2) e può dedurre che nella cella più lontana (2,3) ci sia un'altra zona di rumore ( R ) oppure una zona di pericolo ( P ).
R2,2 ⇒ ( R2,3 ∨ P2,3 )
Nel quadrante (2,1), invece, l'agente non rileva alcun rumore, la zona di silenzio consente di escludere la presenza di un punto di pericolo ( P ) nella cella più lontana (3,1). Quindi, se R2,1 è falsa ¬R2,1 possiamo dedurre che:
¬R2,1 ⇒ ( R3,1 ∨ S3,1 )
La semantica ha consentito di attribuire un valore di verità e un significato alla proposizione logica R, grazie alla quale l'agente razionale può decidere di continuare l'esplorazione in modo intelligente, spostandosi dal quadrante (1,1) al quadrante (2,1). Senza la regola semantica non avrebbe potuto escludere a priori le celle rumorose (1,2) e (2,2), l'esplorazione della mappa sarebbe stata più lunga e più rischiosa.
