Problema di assegnazione
Il problema di assegnazione è una fase del processo di risoluzione dei problemi tramite la tecnica CSP ( Constraint Satisfaction Problem ). La fase consiste nell'assegnazione dei valori alle variabili del problema, al fine di analizzare il risultato finale. I valori di ogni singola variabile devono essere compresi nel relativo dominio ( range di variazione ) della variabile. Ad esempio, dato un modello CSP a tre variabili x1, x2, x3, il dominio di ogni variabile è il seguente:
x1={ 0, 1, 2 }
x2={ 2, 3, 4 }
x3={ 1, 2, 3 }
L'algoritmo CSP deve verificare l'esistenza di una combinazione di valori tale da ottenere una somma x1+x2+x3 pari a 3. Nell'analizzare le varie combinazioni l'algoritmo utilizza esclusivamente i valori compresi nei domini delle variabili. Complessivamente, l'algoritmo elabora 33 combinazioni ed effettua 27 cicli di elaborazione. Ogni ciclo equivale a una specifica operazione di assegnazione dei valori alle variabili. Nel seguente albero di ricerca sono rappresentate le combinazioni delle variabili tenendo conto dei rispettivi domini.
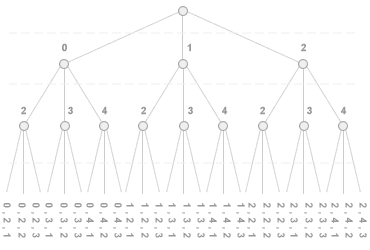
I modelli CSP consentono di ridurre notevolmente il numero delle assegnazioni. In assenza dei domini ( range )delle tre variabili l'algoritmo dovrebbe analizzare infinite combinazioni di numeri interi, molte delle quali sarebbero inutili e inconsistenti. In conclusione, la presenza dei domini ( range ) in un modello CSP consente di ridurre il processo di esplorazione dell'albero di ricerca.
Propagazione dei vincoli. L'efficienza dell'algoritmo CSP può essere ulteriormente migliorata adottando la tecnica della propagazione dei vincoli. In molti problemi CSP il dominio di una variabile influenza e riduce il campo di variazione ( dominio ) delle altre variabili del problema. La propagazione dei vincoli consente di selezionare soltanto i nodi consistenti dell'albero di ricerca ed eliminare dalla ricerca tutti gli altri nodi inconsistenti. Ad esempio, sulla base del valore assunto dalla variabile X1 l'algoritmo può analizzare se la somma X1+X2 eccede il valore 3 ( obiettivo ) e interrompere la ricerca su quel ramo, evitando l'eplorazione completa dell'albero di ricerca. Nella seguente rappresentazione il taglio dei rami dell'albero di ricerca ( taglio di ricerca ) è indicato con il colore rosso.
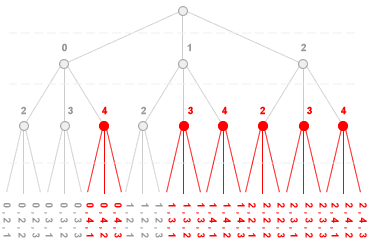
È importante sottolineare che in un nodo inconsistente i valori assegnati alle variabili soddisfano il dominio di ciascuna variabile. Tuttavia, sulla base delle relazioni tra le variabili del modello, si tratta di combinazioni impossibili e quindi inutili da analizzare. Ciò consente di ridurre ulteriormente il numero delle combinazioni da analizzare ( problema di assegnazione ) all'interno di un albero di ricerca. La propagazione dei vincoli può essere effettuata in modo dinamico, mentre l'algoritmo è in esecuzione, oppure in modo preventivo ( ex-ante ) prima dell'inizio della ricerca.
Ordine di assegnazione. L'ordine di assegnazione delle variabili e dei valori delle variabili può influire sensibilmente sull'efficienza della ricerca. Nell'esempio precedente l'ordine di assegnazione delle variabili è x1⇒x2⇒x3. Prima la variabile x1, poi la variabile x2 e, infine, la variabile x3. Potremmo però adottare anche un ordine diverso ( es. x3⇒x2⇒x1 ). Allo stesso modo l'ordine di assegnazione dei valori a una variabile può influire sull'efficienza della ricerca. Ad esempio, nell'esempio precedente il dominio della variabile x1 è { 0, 1, 2 }. L'algoritmo assegna i valori alla variabile x1 seguendo l'ordine 0⇒1⇒2. Viene assegnato alla variabile x1 prima il valore 0, poi il valore 1 e, infine, il valore 2. Modificando l'ordine di presentazione dei valori con { 2, 1, 0 } si modifica anche l'ordine di elaborazione dei valori in 2⇒1⇒0. L'ordine di assegnazione delle variabili e dei valori determina la complessità e il tempo di esecuzione dell'algoritmo di ricerca.
