Consistenza di arco
La consistenza di arco ( arc consistency ) è l'analisi del campo di variazione dei valori ( dominio ) di un nodo ( variabile ) in relazione al vincolo binario con un altro nodo collegato. La consistenza di nodo è un tipo di consistenza locale. Dati due nodi A e B, legati tra loro da un vincolo binario ( arco ), è possibile ridurre il dominio del nodo A in base al dominio del nodo B. Una variabile ( nodo ) è un nodo arco-consistente quando ogni valore del suo dominio soddisfa i vincoli binari con gli altri nodi collegati ( variabili ). Un esempio di consistenza d'arco è la seguente rete con tre nodi-variabili ( A, B, C ) e due vincoli binari ( archi ).
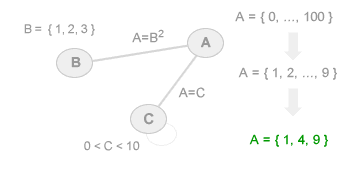
Inizialmente il nodo A ha un dominio pari a { 0, ... , 100 } ed è sottoposto a due vincoli binari. Il vincolo binario tra A e C definisce il dominio del nodo A uguale al nodo C ( A=C ). A sua volta il nodo C è sottoposto a un vincolo unario 0<C<10 che definisce il suo dominio pari a { 1, 2, ... , 9 }. In base al vincolo binario ( A=C ) possiamo ridurre il dominio del nodo A da { 0, ... , 100 } all'insieme dei valori del nodo C { 1, 2, ... , 9 }. L'analisi di consistenza non è ancora finita. Il nodo A è sottoposto anche al vincolo binario con il nodo B che definisce l'uguaglianza tra gli elementi di A con gli elementi di B elevati a potenza ( A = B2 ). Possiamo ridurre ulteriormente il dominio del nodo A ai soli elementi che soddisfano il vincolo A=B2. Essendo il nodo B composto dagli elementi { 1, 2, 3 } possiamo ridurre il dominio del nodo A da { 1, ..., 9 } a { 1, 4, 9 } in cui 1=12 , 4=22 e 9=32. Con il dominio della variabile pari a { 1, 4, 9 } il nodo A è un nodo arco-consistente poiché tutti gli elementi del dominio della variabile A soddisfano i vincoli binari con gli altri nodi collegati ( B e C ).
Propagazione dei vincoli. La consistenza d'arco consente di ridurre il dominio di una variabile, riducendo il numero di cicli dell'algoritmo CSP per elaborare il problema. Nell'esempio precedente la consistenza d'arco della variabile A consente di ottimizzare il lavoro dell'algoritmo CSP, il quale non deve più considerare 100 valori della variabile A ( nodo A ) ma soltanto 3 valori arco-consistenti, riducendo così il numero dei cicli dell'elaborazione.
Rete arco-consistente. Una rete di nodi è detta rete arco-consistente quando tutti i suoi nodi sono nodi arco-consistenti. Ogni nodo ( variabile ) della rete ( sistema ) soddisfa il criterio di consistenza nei confronti degli altri nodi collegati ( variabili ).
Arco orientato di consistenza. Un problema CSP si dice arco orientato di consistenza quando, dato un ordinamento delle variabili ( x1, x2, ... , xn ) se ogni xi è arco consistente con ogni xj per j>i.
