Analisi delle corrispondenze lessicali ( LCA )
L'analisi delle corrispondenze lessicali è l'applicazione ai testi dell'analisi fattoriale delle corrispondenze. È conosciuta anche con l'acronimo inglese LCA ( Lexical Correspondence Analysis ). Il metodo viene elaborato dal francese J.P. Benzécri negli anni '80, prendeno spunto dall'analisi delle co-occorrenze di Osgood.
Come funziona l'analisi LCA
L'oggetto di indagine dell'analisi è un insieme di testi ( T1, T2, T3, ecc. ) che costituisce il corpus da analizzare.

Si costruisce una tabella a doppia entrata ponendo sulle colonne i testi e sulle righe i termini, o forme lessicali, presenti all'interno dei vari testi. Nelle celle in cui si incontra una riga ( termine ) con una colonna ( testo ) viene inserito il numero di volte che il termine compare nel testo in questione, ossia la sua frequenza assoluta.
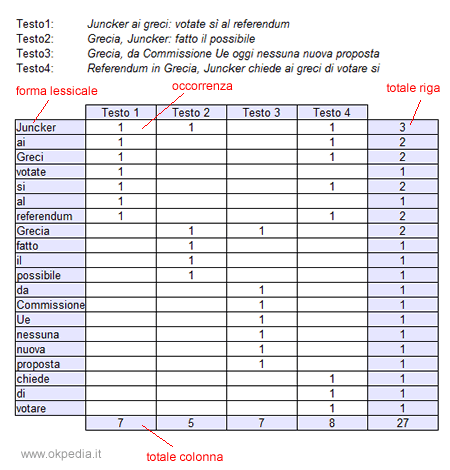
Ai margini della tabella si calcolano i totali della riga e della colonna. Questi totali sono utili per trasformare le frequenze assolute delle occorrenze in frequenze relative.
Le frequenze relative delle occorrenze lessicali
Il rapporto tra la frequenza assoluta dell'occorrenza lessicale di una parola in un testo e il totale della colonna consente di ottenere il peso del termine rispetto agli altri termini del testo.
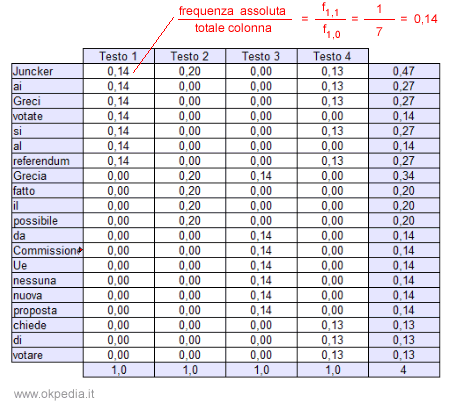
Il rapporto tra la frequenza assoluta dell'occorrenza lessicale di una parola in un testo e il totale della riga consente di calcolare la distribuzione del termine nei vari testi del corpus.
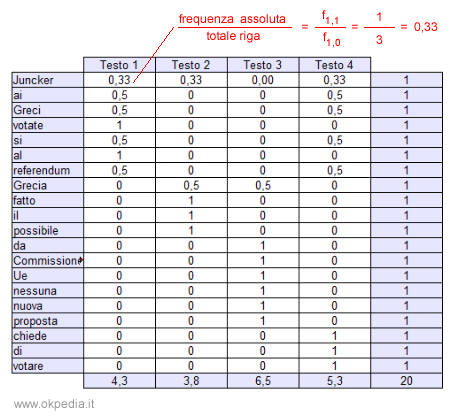
Le frequenze relative consentono il confronto delle distribuzioni lessicali tra i testi, indipendentemente dal numero delle parole.
Ad esempio, quando due testi hanno una distribuzione simile delle frequenze relative lessicali, i due testi si somigliano poiché sono composti dalle stesse parole.
Come verificare il grado di somiglianza dei testi
I testi sono trasformati in vettori per ciascuna colonna ( testo ). Ogni elemento del vettore indica la frequenza relativa di un termine all'interno del testo. In questo modo, il vettore fornisce un'immagine matematica della distribuzione lessicale del testo.

La differenza tra gli elementi di due vettori di colonna permette di calcolare il grado di somiglianza dei testi ed evidenziare le parti del testo differenti.
Uno degli indicatori statistici per misurare il grado di differenza è il chi-quadrato. Il chi-quadrato si calcola sommando il quadrato della differenza delle frequenze relative corrispondenti nei due vettori. La somma viene divisa con il numero degli elementi dei vettori.
Se la differenza tra i due vettori tende a zero, i due testi hanno un grado elevato di affinità. In estrema ipotesi, se la differenza tra i due vettori è uguale a zero, i due testi sono identici.
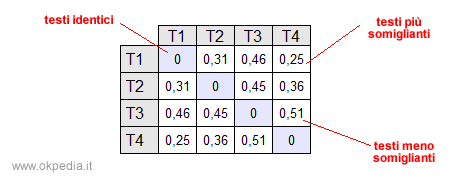
Ad esempio, nella precedente tabella di Okpedia abbiamo calcolato il chi-quadrato di tutte le combinazioni dei testi. Il confronto tra i testi uguali ( es. T1 con T1, T2, con T2, ecc. ) è uguale a zero.
- Il valore chi-quadrato più basso ( χ = 0,25 ) si rileva nel confronto tra i testi T1 e T4. All'interno del corpus i testi T1 e T2 sono quelli che si somigliano di più.
- Il valore chi-quadrato più alto ( χ = 0,51 ), invece, si rileva nel confronto tra i testi T3 e T4. All'interno del corpus i testi T3 e T4 sono quelli che si somigliano di meno.
La distribuzione di una forma lessicale nel corpus dei testi
La distribuzione di un termine nei vari testi consente, invece, di conoscere il peso della forma lessicale nel corpus generale dei testi. In questo caso il vettore non è composto dalle frequenze relative dei termini di un testo, bensì dalla distribuzione di un termine nel corpus dei testi.
Ad esempio, prendiamo un campione composto da quattro forme lessicali ( K1, K2, K3, K4 ) e analizziamo la relazione che hanno all'interno del corpus.

Calcolando il chi-quadrato su tutte le combinazioni delle forme lessicali ( Kn ) si possono individuare i testi con un grado di somiglianza maggiore ( chi-quadrato più basso ).
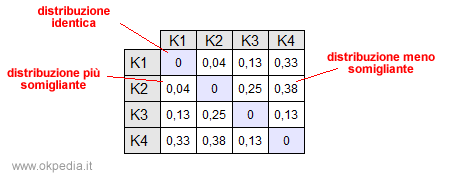
I termini K1 e K2 hanno una distribuzione più somigliante nel corpus dei testi e, quindi, potrebbero veicolare un particolare significato. Viceversa, i termini K2 e K4 sono quelli più distanti nel corpus.
L'analisi del grado lessicale di vicinanza
L'analisi delle corrispondenze lessicali può essere effettuata anche calcolando la distanza le distribuzioni delle frequenze lessicali nei testi ( T1, T2, T3, T4 ) e una distribuzione attesa presa come riferimento ( Dx ).
Ad esempio, in un particolare argomento co-occorrono delle forme lessicali con lo stesso peso. Questa distribuzione attesa consente di individuare i testi del corpus con un grado lessicale di vicinanza più alto ( chi-quadrato più basso ).

Quando due vettori lessicali ( testi ) hanno una distribuzione simile a quella attesa, probabilmente affrontano lo stesso argomento nello stesso campo semantico.
L'analisi delle corrispondenze lessicali è utile anche per focalizzare l'attenzione su alcuni aspetti da raggruppare in cluster ( raggruppamento ) e sulla relazione tra i cluster e altri termini ( argomenti ) oggetto dell'analisi.
L'analisi dei cluster è generalmente rappresentata sui quattro semipiani degli assi cartesiani.
