Vettore

I vettori sono quantità caratterizzate sia dalla magnitudine che dalla direzione. In uno spazio bidimensionale o tridimensionale, un vettore è rappresentato come una freccia di lunghezza specifica, che parte da un punto iniziale (O) e termina in un punto (x,y).

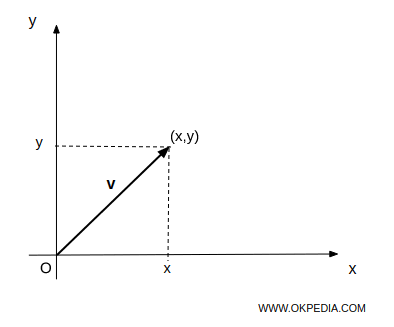
Un vettore libero (o semplicemente vettore) è una classe di segmenti orientati equipollenti.

Due o più segmenti orientati hanno una relazione di equipollenza ( equivalenza ) quando hanno lo stesso modulo, direzione e verso.

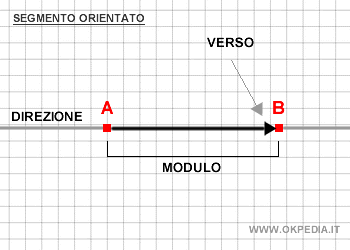
• Il modulo è la lunghezza del vettore. È un valore positivo espresso in un'unità di misura di riferimento.
• La direzione è la retta in cui si trova il vettore stesso.
• Il verso è l'orientazione del vettore ed è indicato tramite un freccia.

L'analisi reale dei vettori a due o più dimensioni è oggetto di studio del calcolo vettoriale, uno dei rami dell'algebra lineare che si occupa di studiare le grandezze vettoriali.

Cosa sono le grandezze vettoriali? Le grandezze vettoriali sono grandezze esprimibili tramite un modulo ( lunghezza o intensità ), una direzione e un verso. Si distinguono dalle grandezze scalari che, invece, sono esprimibili da numeri reali in un'unità di misura.

Un esempio di vettore

I segmenti orientati u, v, w appartengono allo stesso vettore libero perché hanno la stessa direzione, verso e modulo (lunghezza).

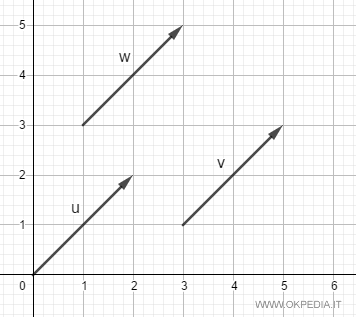
Fanno parte della stessa classe di equipollenza ( equivalenza ).

I tre segmenti orientati si distinguono soltanto per l'origine.

Vettore di posizione e di spostamento

Possiamo distinguere diversi concetti legati al termine vettore, tra questi i seguenti:

• Vettore posizione. Il vettore posizione individua la posizione di un punto nello spazio rispetto a un sistema di riferimento.
  
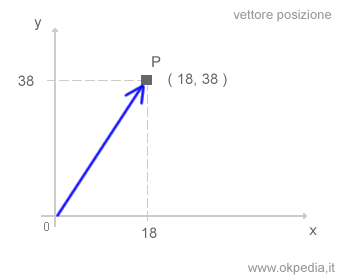
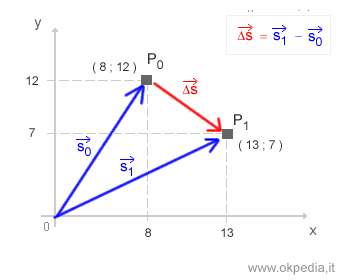
• Vettore spostamento. Il vettore spostamento è rappresentato da un freccia che ha origine nel posizione iniziale del punto materiale e la punta nella posizione finale. Esprime la variazione del vettore di posizione.
  

Operazioni sui vettori

I vettori possono essere soggetti a varie operazioni, tra cui l'addizione, la sottrazione e la moltiplicazione per uno scalare.

Ognuna di queste operazioni ha regole e proprietà specifiche che determinano la magnitudine e la direzione del vettore risultante.

Le principali operazioni che coinvolgono i vettori includono:

• Addizione di vettori
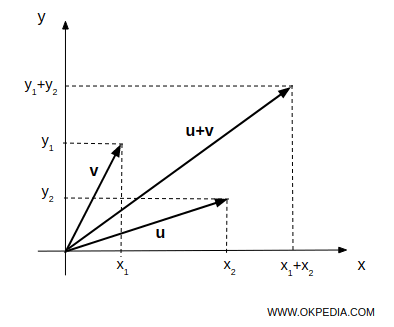
  Se (x₁,y₁) e (x₂,y₂) sono i punti finali di due vettori, u e v rispettivamente, allora (x₁+x₂,y₁+y₂) è il punto finale del vettore u+v.
  
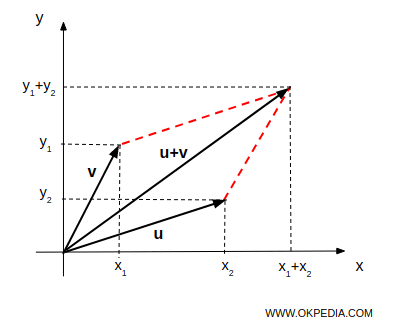
  La somma di due vettori nello spazio R²=RxR può essere determinata anche usando il metodo del parallelogramma.
  
• Moltiplicazione per uno scalare
  Se (x, y) è il punto finale del vettore v, allora il prodotto kv risulta in un vettore con il punto finale (kx, ky).
  
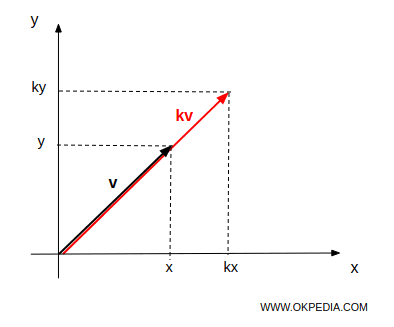
  Il prodotto di un numero reale k e un vettore v si ottiene moltiplicando la magnitudine di v per k. Questo prodotto mantiene la stessa direzione se k > 0, o inverte la direzione se k < 0.

Vettori con più di due dimensioni

Un vettore multidimensionale è essenzialmente una lista ordinata di n valori. Questi possono essere concettualizzati come una n-upla di numeri reali. Ogni valore è indicato da un simbolo con un pedice che ne rappresenta la posizione nella lista, ad esempio, x₁, x₂, ..., x_n.

La notazione dei vettori utilizza tipicamente una lettera con una freccia sopra, rappresentata come

$$ \vec{v} = ( x_1 \ , \ x_2 \ , ... , \ x_n ) $$

I vettori sono fondamentali per rappresentare quantità che non possono essere descritte con un solo valore. In fisica, una forza è un esempio pratico di una grandezza vettoriale.

Nota. Su Okpedia, i vettori sono distinti dagli scalari presentandoli in grassetto. Ad esempio, u, w e v sono vettori, mentre u, v e w sono scalari.

---

Altri significati di vettore

• Vettore ( informatica ). Nell'informatica il vettore è un'unica variabile che contiene al suo interno un insieme di elementi omogenei. Gli elementi del vettori sono associati a un indice per poterli reperire nella posizione di memoria ove sono registrati.
• Vettore ( computer grafica ). Il termine vettore è utilizzato con un significato diverso nella computer grafica, dove indica un insieme di valori o parametri ( es. posizione dei vertici colori, ecc. ) che permettono di rappresentare le immagini degli oggetti tridimensionali.