Prodotto scalare tra vettori

Dati due vettori \( x = (x_1, x_2, \ldots, x_n) \) e \( y = (y_1, y_2, \ldots, y_n) \) in \( \mathbb{R}^n \), il prodotto scalare, detto anche prodotto interno (o dot product), è definito come: \[ \langle x, y \rangle = \sum_{i=1}^n x_i y_i \] ossia \[ \langle x, y \rangle = x_1 y_1 + x_2 y_2 + \ldots + x_n y_n \]

È un'operazione che restituisce un numero reale (uno scalare), non un vettore.

Dal punto di vista geometrico, il prodotto scalare può essere espresso anche in termini di angolo tra i due vettori:

\[ \langle x, y \rangle = \|x\| \cdot \|y\| \cdot \cos\theta \]

Dove \( \|x\| \) e \( \|y\| \) sono le norme dei due vettori, mentre \( \theta \) è l'angolo compreso tra i due vettori (tra 0° e 180°).

Il prodotto scalare è particolarmente utile per trovare l'angolo tra i vettori e per verificare l'ortogonalità dei vettori \( \langle x, y \rangle = 0 \Rightarrow x \perp y \)

Proprietà del prodotto scalare

Il prodotto scalare soddisfa queste proprietà:

• Commutatività
  L’ordine dei due vettori non cambia il risultato del prodotto scalare. \[ \langle x, y \rangle = \langle y, x \rangle\]
• Linearità
  il prodotto scalare è lineare rispetto alla somma e alla moltiplicazione per scalari. È utile per scomporre combinazioni lineari di vettori. \[ \langle ax + bz, y \rangle = a\langle x, y \rangle + b\langle z, y \rangle \quad \text{per ogni } a, b \in \mathbb{R} \]
• Positività
  Il prodotto scalare di un vettore con sé stesso è sempre positivo o nullo, ed è nullo solo se il vettore è nullo. Serve come base per definire la lunghezza (norma) dei vettori. \[ \langle x, x \rangle = \|x\|^2 \geq 0 \quad \text{e } \langle x, x \rangle = 0 \iff x = 0 \]

Esempio pratico

Vediamo passo passo il calcolo del prodotto scalare tra due vettori, della norma e infine del coseno dell’angolo tra di essi.

Siano dati i due vettori nel piano:

\[ x = (2, 3), \quad y = (4, -1) \]

Applichiamo la definizione del calcolo del prodotto scalare

\[ \langle x, y \rangle = x_1 y_1 + x_2 y_2 \]

Sostituendo i valori:

\[ \langle x, y \rangle = 2 \cdot 4 + 3 \cdot (-1) = 8 - 3 = 5 \]

Quindi, il prodotto scalare tra \( x \) e \( y \) è 5.

Ora vediamo come si calcola l'angolo tra i due vettori.

Dalla formula geometrica del prodotto scalare ricaviamo il coseno dell'angolo.

\[ \langle x, y \rangle = \|x\| \cdot \|y\| \cdot \cos\theta \]

Il coseno dell’angolo tra \( x \) e \( y \) è dato dal rapporto tra il prodotto scalare e il prodotto delle norme.

\[ \cos\theta = \frac{\langle x, y \rangle}{\|x\| \cdot \|y\|} = \frac{5}{\sqrt{13} \cdot \sqrt{17}} \]

La norma (o modulo) si calcola come:

\[ \|x\| = \sqrt{x_1^2 + x_2^2} \]

Quindi, la lunghezza del vettore \( x \) è \( \sqrt{13} \).

La norma di \( y \) è

\[ \|y\| = \sqrt{y_1^2 + y_2^2} = \sqrt{4^2 + (-1)^2} = \sqrt{16 + 1} = \sqrt{17} \]

Pertanto, la lunghezza del vettore \( y \) è \( \sqrt{17} \).

Una volta ottenuti questi valori calcoliamo il coseno dell’angolo tra \( x \) e \( y \)

\[ \cos\theta = \frac{\langle x, y \rangle}{\|x\| \cdot \|y\|} = \frac{5}{\sqrt{13} \cdot \sqrt{17}} \]

Poiché \( \cos\theta > 0 \), l’angolo tra i vettori è acuto (cioè minore di 90°).

Calcoliamo i valori approssimati delle radici \( \sqrt{13} \approx 3.6056 \) e \( \sqrt{17} \approx 4.1231 \)

\[ \cos\theta \approx \frac{5}{3.6056 \cdot 4.1231} = \frac{5}{14.867} \approx 0.3362 \]

Ora calcoliamo l’arcocoseno cioè l’angolo il cui coseno è 0.3362:

\[ \theta \approx \arccos(0.3362) \approx 70.35^\circ \]

In conclusione, l'angolo tra i due vettori è \( \theta \approx 70.35^\circ \)

Poiché è maggiore di 45° ma minore di 90°, i vettori formano un angolo acuto non troppo stretto.

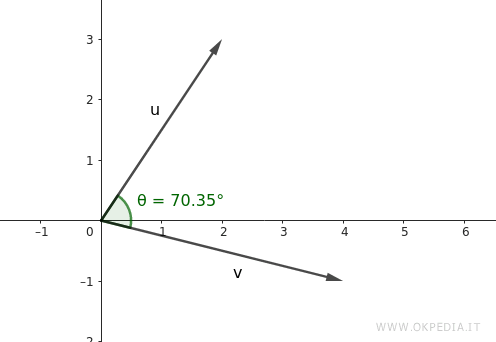
Questo esempio mostra chiaramente il legame tra la forma algebrica e la forma geometrica del prodotto scalare.