Vettore spostamento
Il vettore spostamento è la variazione di un punto materiale P in un intervallo di tempo. Esprime la variazione ( o spostamento ) di un vettore di posizione nel tempo.
Come calcolare un vettore spostamento
All'istante t0 il punto materiale si trova nella posizione P0 ( nelle coordinate (8;12). Il vettore di posizione S0 è indicato da una freccia che congiunge l'origine del diagramma cartesiano con il punto P0.
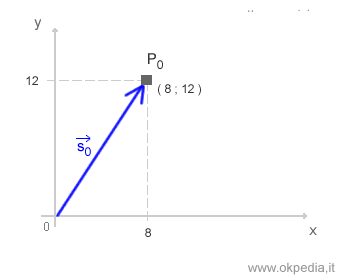
Nell'istante successivo t1 il punto materiale occupa una nuova posizione nel piano ( P1 ) alle coordinate (7;13). Il nuovo vettore di posizione S1 è rappresentato da una freccia che congiunge l'origine degli assi cartesiano con il punto P1.
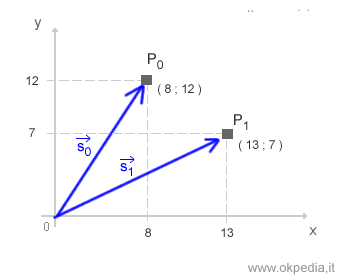
Lo spostamento del punto materiale nel tempo viene indicato con un vettore spostamento pari alla differenza tra i due vettori di posizione S1 e S0.
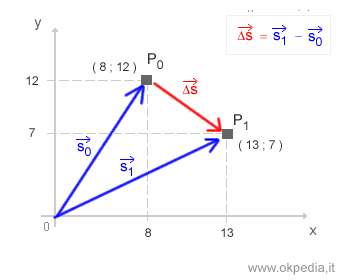
Il vettore spostamento ci indica la direzione, il verso e la lunghezza ( modulo ) del moto del punto. La direzione e il verso sono già evidenti nel grafico. Nel prossimo paragrafo vedremo come calcolare la lunghezza, ossia il modulo del vettore.
Come calcolare geometricamente la lunghezza ( modulo ) del vettore spostamento
Per calcolare la lunghezza del vettore spostamento dobbiamo eseguire la differenza tra i due vettori di posizione. Essendo il vettore s0 il sottraendo, si deve disegnare il suo opposto alle coordinate (-8;-12).
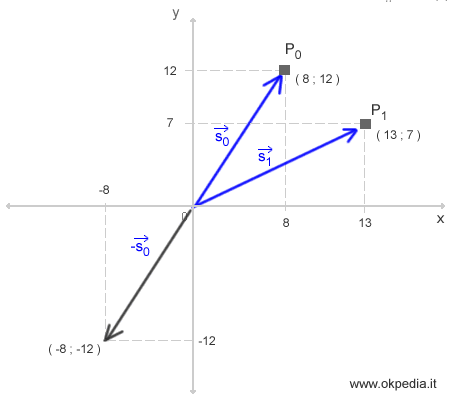
Il nuovo vettore -s0 ( sottraendo ) ha la stessa direzione di s0 ma senso opposto e ci consente di costruire un parallelogramma insieme al vettore s1 ( minuendo ). Questo ci permette di tracciare il vettore spostamento a partire dall'origine O.
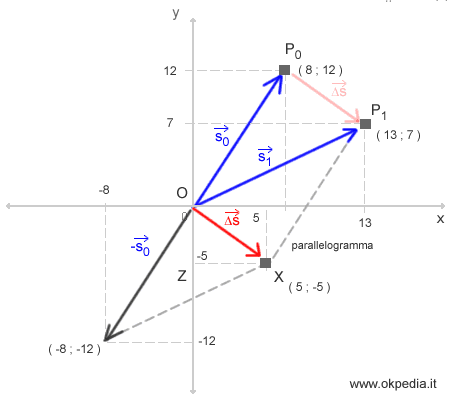
Come si può notare, il vettore OX è uguale al vettore P0P1. Per calcolare la lunghezza del vettore spostamento OX è sufficiente applicare il teorema di Pitagora: l'ipotenusa OX è uguale alla radice quadrata della somma dei quadrati dei cateti OZ2+ZX2.
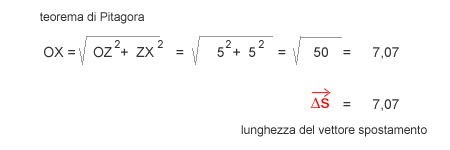
Abbiamo calcolato il modulo del vettore spostamento ossia la lunghezza. In questo caso, il vettore spostamento ΔS ha una lunghezza pari a 7,07.
Un metodo rapido di calcolo della lunghezza
Avremmo potuto calcolare la lunghezza del vettore spostamento in modo più rapido, utilizzando il teorema di Pitagora direttamente sul triangolo composto dai vettori posizione. Ogni cateto è uguale al modulo della differenza delle coordinate dei punti rispetto a un asse.
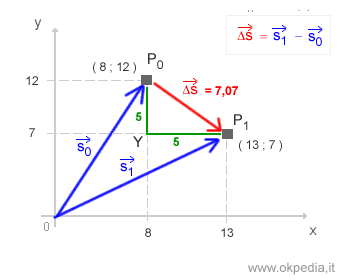
Ad esempio, il cateto YP1 è uguale a |13-8| = 5 rispetto all'asse cartesiano delle ascisse (X). Il cateto YP0 è, invece, uguale a |7-12|=5 rispetto all'asse cartesiano delle ordinate (Y).
Come ricostruire la traiettoria del moto
Lo spostamento è la differenza dei vettori posizione. Il vettore spostamento ΔS ci consente di capire come è avvenuto il moto dello spostamento ( direzione, verso e lunghezza ) del punto materiale P nell'intervallo temporale Δt intercorso tra l'istante t0 e l'istante t1.
Δt = t1-t0
Il calcolo del vettore spostamento in un intervallo temporale ci permette di determinare di ricostruire la traiettoria seguita dal punto nel suo spostamento.
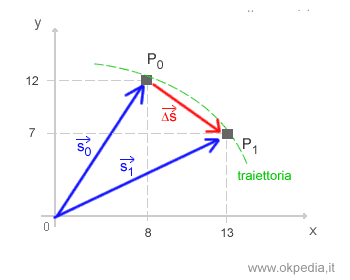
Quanto più è piccolo l'intervallo temporale Δt, tanto più la ricostruzione della traiettoria reale è precisa. Ad esempio, nella seguente figura di okpedia sono rappresentati due vettori spostamento.
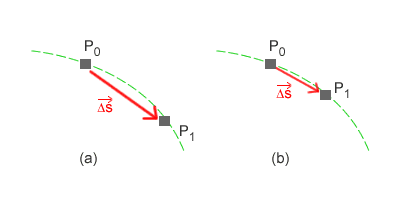
Il vettore (b) congiunge due punti più vicini e la freccia del vettore spostamento ( rossa ) è più vicina alla curva della traiettoria ( verde ) rispetto al vettore (a). È quindi più preciso.
In un intervallo temporale infinitamente piccolo il vettore spostamento coincide con la retta tangente della traiettoria nel punto materiale P.
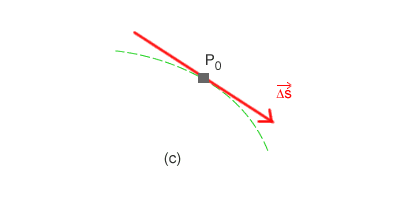
Ad esempio, nella precedente figura di okpedia il vettore spostamento (c) è rilevato in un intervallo di tempo molto piccolo, infinitamente piccolo, e la freccia di spostamento è tangente alla traiettoria nel punto P.
