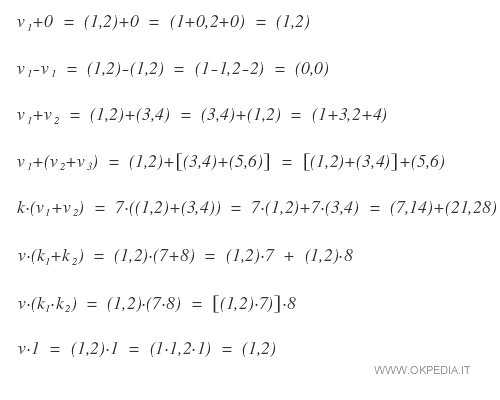Spazio vettoriale

Definizione

Uno spazio vettoriale è una struttura algebrica composta da un insieme di scalari ( detto campo ), un insieme di vettori e da due operazioni binarie (somma e moltiplicazione per uno scalare) caratterizzate da determinate proprietà. È anche detto spazio lineare.

Gli elementi dello spazio vettoriale sono i seguenti:

• Campo
  Un insieme K di numeri scalari. Ad esempio, il campo dei numeri reali R o dei numeri complessi C.
  
  
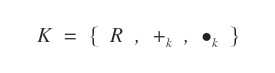
  I campi più frequenti sono:
  • Spazio vettoriale reale, se il campo K è l'insieme dei numeri reali (R).
  • Spazio vettoriale complesso, se il campo K è l'insieme dei numeri complessi (C).
• Vettori
  Un insieme V non vuoto di vettori.
  
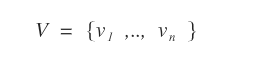
• Somma e moltiplicazione per scalare
  Due operazioni binarie (somma e prodotto per scalare) che rispettano le seguenti proprietà dove k è uno scalare e v è un vettore.
  1. elemento neutro
     v+0=v
  2. elemento opposto
     v-v=0
  3. associativa
     v₁+(v₂+v₃)=(v₁+v₂)+v₃
  4. commutativa
     v₁+v₂=v₂+v₁
  5. distributiva del prodotto per scalare
     k·(v₁+v₂)=k·v₁+k·v₂
  6. pseudo distributiva
     v·(k₁+k₂)=v·k₁+v·k₂
  7. pseudo associativa
     v·(k₁k₂)=k₁(v·k₂)=k₂(k₁·v)
  8. elemento neutro del prodotto
     v*1=v

Esempio

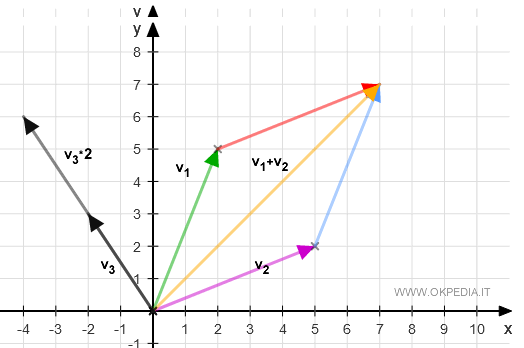
Lo spazio vettoriale dei punti (x,y) del piano cartesiano a due dimensioni è uno spazio vettoriale RxR=R² nel campo K dei numeri reali.

Ogni coordinata (x,y) del piano è un vettore v rispetto all'origine (O).

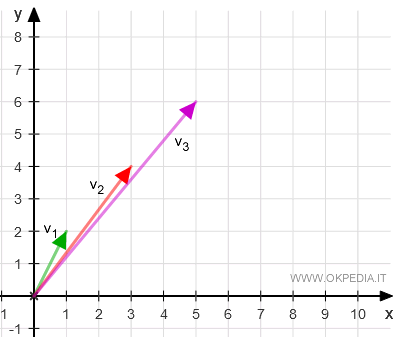
Nello spazio vettoriale sono definite le operazioni binarie della somma (v₁+v₂) e del prodotto per lo scalare (k·v).

Prendiamo due scalari k qualsiasi dall'insieme dei numeri reali (k₁,k₂) e tre vettori qualsiasi (v₁,v₂,v₃) dall'insieme dei vettori V dello spazio vettoriale.

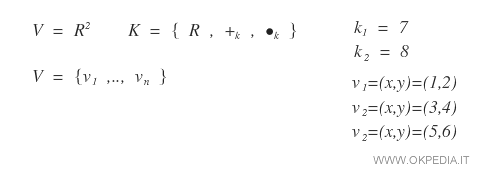
Le due operazioni binarie rispettano tutte le proprietà degli spazi vettoriali.