Distanza tra due vettori

Dati due vettori nello spazio euclideo \( \mathbb{R}^n \):\[\vec{x} = (x_1, x_2, \ldots, x_n) \] \[ \vec{y} = (y_1, y_2, \ldots, y_n)\] La distanza euclidea tra \( x \) e \( y \) è definita come la radice quadrata della somma dei quadrati delle differenze tra le rispettive componenti. \[ \text{dist}(\vec{x}, \vec{y}) = \| \vec{x} - \vec{y} \| \] \[ = \sqrt{(x_1 - y_1)^2 + \ldots + (x_n - y_n)^2}\]

La distanza euclidea è la lunghezza del segmento che unisce i vettori \( x \) e \( y \) nello spazio.

È un'applicazione diretta del teorema di Pitagora in \( n \) dimensioni.

Esempio

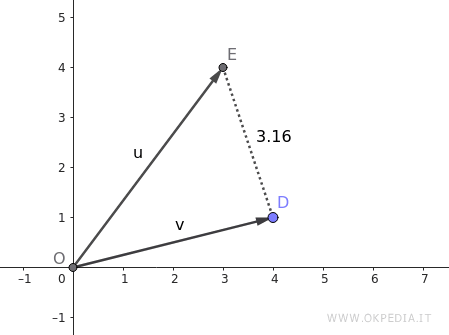
Consideriamo de vettori:

\[ \vec{u} = (3, 4) \]

\[ \vec{v} = (4, 1 ) \]

La distanza tra i due vettori è 3.16

\[
\text{dist}( \vec{u} , \vec{v} ) = \sqrt{(3 - 4)^2 + (4 - 1)^2} = \sqrt{1 + 9} = \sqrt{10} = 3.16
\]

In questo caso, il vettore \( \vec{u} \) si trova a distanza 5 dal vettore \( \vec{v} \).

Proprietà della distanza euclidea

Le proprietà della distanza euclidea tra due vettori sono le seguenti:

• Simmetria
  La distanza tra due punti non dipende dall'ordine con cui vengono considerati: andare da \( x \) a \( y \) o da \( y \) a \( x \) richiede lo stesso "spostamento" nello spazio. \[ \text{dist}(x, y) = \text{dist}(y, x) \]
• Positività
  La distanza tra due punti è sempre maggiore o uguale a zero, e vale esattamente zero solo quando i due punti coincidono. \[ \text{dist}(x, y) \geq 0 \quad \text{e} \quad \text{dist}(x, y) = 0 \iff x = y \]
• Disuguaglianza triangolare
  Questa proprietà; esprime che la distanza diretta tra due punti è sempre minore o uguale alla somma delle distanze passando per un terzo punto. In altre parole, il percorso più breve tra due punti è la linea retta.
  \[ \text{dist}(x, z) \leq \text{dist}(x, y) + \text{dist}(y, z) \]

Queste proprietà rendono la distanza euclidea una metrica, cioè una funzione che misura "quanto sono distanti due punti".