Norma di un vettore
La norma di un vettore, detta anche modulo o lunghezza, è una funzione che associa a un vettore un numero reale non negativo, che rappresenta la lunghezza del vettore nello spazio \(\mathbb{R}^n\). Ad esempio, se abbiamo un vettore \( x = (x_1, x_2, \ldots, x_n) \), la sua norma euclidea è: \[ \|x\| = \sqrt{x_1^2 + x_2^2 + \cdots + x_n^2} \]
La norma euclidea è una generalizzazione del teorema di Pitagora allo spazio n-dimensionale.
Dal punto di vista geometrico, la norma rappresenta la distanza del vettore dall'origine. Se disegniamo il vettore \( x \) partendo dall'origine \( O \), allora \( \|x\| \) è la distanza tra \( O \) e il punto finale del vettore.
Esempio
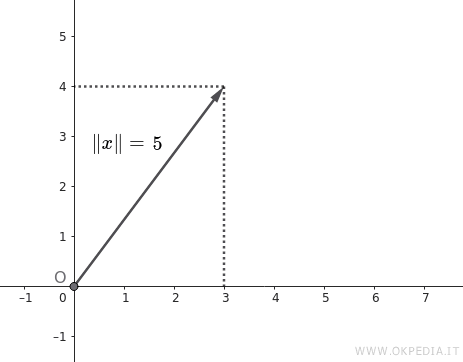
Nello spazio \(\mathbb{R}^2\) consideriamo il vettore \( x = (3, 4) \).
La norma euclidea del vettore è 5
\[ \|x\| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
E' la distanza tra il punto (3,4) e l'origine (0,0) del piano cartesiano.
Altri tipi di norma. Anche se la norma euclidea è la più comune, ci sono altre norme importanti che si usano in contesti diversi, ad esempio:
- Norma \( \ell^1 \) (detta "norma Manhattan"): \[ \|x\|_1 = |x_1| + |x_2| + \cdots + |x_n| \]
- Norma \( \ell^\infty \) (norma del massimo): \[ \|x\|_\infty = \max \{ |x_1|, |x_2|, \ldots, |x_n| \} \]
Relazione con il prodotto scalare
La norma di un vettore può essere espressa in termini di prodotto scalare in questo modo:
\[ \|x\| = \sqrt{\langle x, x \rangle} \]
Quindi, per calcolare la lunghezza (norma) di un vettore \( x \), possiamo semplicemente fare il prodotto scalare del vettore con se stesso, e poi prendere la radice quadrata del risultato.
Prendiamo un vettore in \( \mathbb{R}^n \):
\[ x = (x_1, x_2, \ldots, x_n) \]
Il prodotto scalare tra \( x \) e sé stesso è:
\[ \langle x, x \rangle = x_1 \cdot x_1 + x_2 \cdot x_2 + \ldots + x_n \cdot x_n = x_1^2 + x_2^2 + \cdots + x_n^2 \]
Ma questa è proprio la somma dei quadrati delle componenti del vettore, cioè la quantità che compare dentro la radice nella definizione classica della norma:
\[ \|x\| = \sqrt{x_1^2 + x_2^2 + \cdots + x_n^2} \]
Quindi possiamo riscrivere tutto così:
\[ \|x\| = \sqrt{\langle x, x \rangle} \]
Le proprietà della norma
La norma soddisfa le seguenti proprietà:
- Positività
La norma è sempre maggiore o uguale a zero, ed è zero solo se il vettore è nullo. \[ \|x\| \geq 0 \quad \text{e} \quad \|x\| = 0 \iff x = 0 \] - Omogeneità (moltiplicazione per uno scalare)
Se moltiplichiamo un vettore per un numero, la sua norma viene moltiplicata per il valore assoluto di quel numero. \[ \|\lambda x\| = |\lambda| \cdot \|x\| \] - Disuguaglianza triangolare
La norma della somma di due vettori è minore o uguale alla somma delle loro norme: è come dire che "il percorso più diretto è sempre il più corto". \[ \|x + y\| \leq \|x\| + \|y\| \]
