Congruenza di figure geometriche
La definizione di congruenza
Due figure geometriche A e B sono congruenti quando sono sovrapponibili punto a punto dopo un movimento rigido.
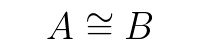
La congruenza è una relazione di equivalenza ed è indicata con il simbolo uguale con una linea curva superiore.
Un esempio di congruenza
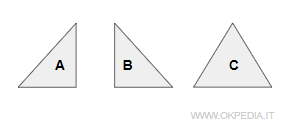
Questi due triangoli sono congruenti perché sovrapponibili con un movimento rigido ( spostamento ).
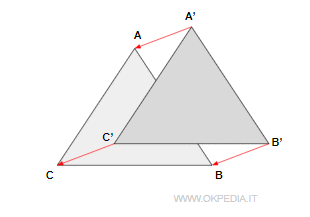
Nell'immagine seguente le figure A e B sono congruenti perché sovrapponibili dopo due movimenti rigidi ( ribaltamento e spostamento ) mentre le figure A e C non sono congruenti.
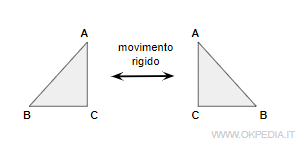
Cos'è un movimento rigido
Nella geometria euclidea per movimento rigido si intende uno spostamento della figura geometrica senza deformazione.
Esempio di movimento rigido. La rotazione di una figura geometrica per 90° è un movimento rigido. Spostare una figura nello spazio è un movimento rigido. Ribaltare una figura geometrica orizzontalmente o verticalmente è un altro movimento rigido.
Differenza tra congruenza e uguaglianza
L'uguaglianza si verifica quando due figure geometriche sono coincidenti punto a punto, ossia condividono gli stessi punti nello spazio.
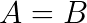
Nei casi di uguaglianza non c'è alcun movimento rigido.
Viceversa, nella congruenza le due figure geometriche non condividono tutti gli stessi punti o nessuno, ma sono sovrapponibili dopo uno o più movimenti rigidi.
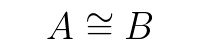
La congruenza è sinonimo di sovrapponibilità.
Nota. L'uguaglianza si indica con il simbolo uguale ( = ). Mentre la congruenza con il simbolo uguale e una linea curva superiore.
Esempio di uguaglianza e congruenza geometrica
In un triangolo isoscele ABC la mediana e l'altezza del triangolo sono uguali perché condividono gli stessi punti del piano ( la retta rossa h ).
E' un esempio di uguaglianza geometrica.
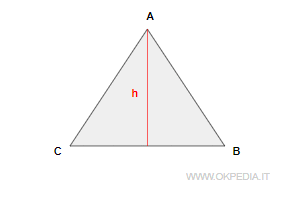
Viceversa, i lato AC e BC del triangolo sono congruenti perché non condividono gli stessi punti ma sono sovrapponibili con un movimento rigido.
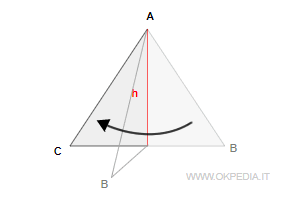
E' un esempio classico di congruenza geometrica.
Le proprietà della congruenza
La congruenza rispetta le seguenti proprietà:
- Proprietà riflessiva. Ogni figura geometrica è congruente con se stessa.
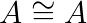
- Proprietà simmetrica. Se la figura A è congruente con la figura B allora la figura B è congruente con la figura A.
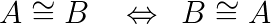
- Proprietà transitiva. Se la figura A è congruente con B e la figura B è congruente con C, allora la figura A è congruente con C.
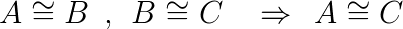
Postulati della congruenza. Esistono diversi postulati sulla congruenza geometrica. Ad esempio, tutte le rette sono congruenti fra loro. Gli angoli piatti sono congruenti tra loro. I semipiani sono congruenti tra loro. Le semirette sono congruenti tra loro. E altri ancora.
