Retta ( geometria )
In geometria la retta ( o linea retta ) è uno degli enti geometrici fondamentali della geometria di Euclide e uno degli enti geometrici primitivi.
La retta è composta da infiniti punti e si estende illimitatamente in entrambe le direzioni. È priva di spessore ed esiste soltanto in una dimensione ( la lunghezza )
I postulati di appartenenza della retta
La definizione della retta deriva da tre postulati di appartenenza della retta.
-
Primo postulato
In due punti distinti di un piano passa una e una sola retta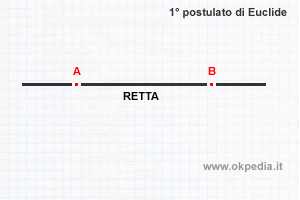
- Con il termine una e una sola retta sono riassunti due concetti:
- Esistenza. Dati due punti esiste una retta che passa per quei punti.
- Unicità. La retta che passa per due punti è unica. Non ne esistono altre.
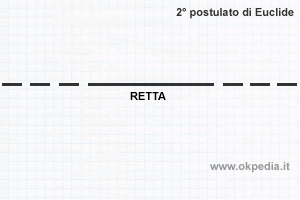
- Secondo postulato
In una retta ci sono almeno due punti - Terzo postulato
Per ogni retta di un piano esiste almeno un punto che non appartiene alla retta
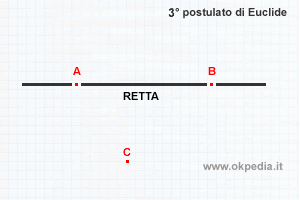
Nota. Questo postulato vuol dire che una retta esiste soltanto sul piano in uno spazio a due o più dimensioni.
La rappresentazione
Nelle rappresentazioni grafiche le rette sono generalmente indicate con le lettere minuscole dell'alfabeto latino.
Il postulato dell'ordine della retta
Secondo il postulato dell'ordine
- La retta è un insieme ordinato di punti.
- Non esiste un primo e un ultimo punto.
La retta è illimitata. - Dati due punti qualsiasi della retta, esiste sempre un altro punto intermedio.
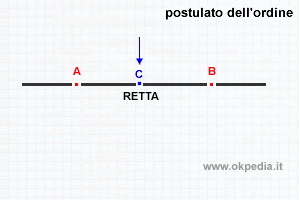
Quindi, la retta è composta da infiniti punti.
Fascio proprio di rette
Il fascio proprio è l'insieme delle rette passanti per un punto del piano.
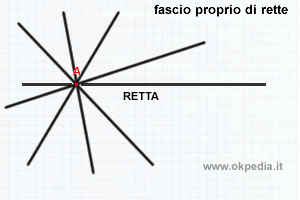
Un piano è composto da infiniti punti.
Pertanto, in ogni punto del piano passano infinite rette.
La retta orientata
La retta orientata è una retta a cui è stato fissato un verso di percorrenza.
Il verso è indicato con una freccia.
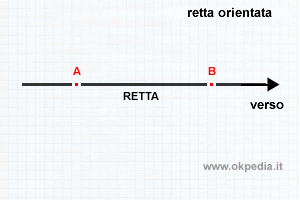
Dati due punti qualsiasi A e B della retta orientata, è sempre possibile dire che A precede o segue B.
Le rette incidenti, parallele, coincidenti
Date due rette, sul piano queste possono essere tra loro incidenti, parallele o coincidenti.
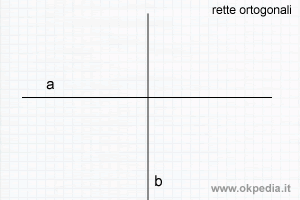
- Rette incidenti. Le rette sono incidenti quando hanno in comune un solo punto. Se le rette incidenti dividono il piano in quatto parti uguali sono dette rette ortogonali / perpendicolari.
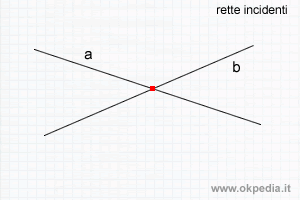
- Rette parallele. Le rette sono parallele quando non hanno in comune nemmeno un punto.
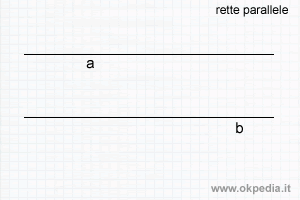
- Rette coincidenti. Le rette sono coincidenti quando hanno in comune tutti i punti.
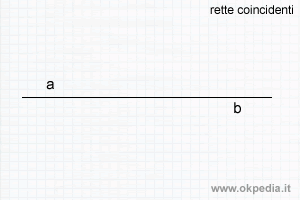
Le rette complanari
Nello spazio a tre o più dimensioni le rette possono essere complanari o sghembe.
- Rette complanari. Le rette sono complanari quando i punti appartengono allo stesso piano. Le rette complanarsi possono intersecarsi o essere parallele.
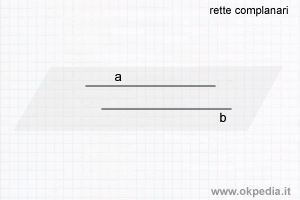
- Rette sghembe. Le rette sono sghembe se non sono contenute in un piano comune. Le rette sghembe non hanno punti in comune, non sono parallele e non possono intersecarsi.
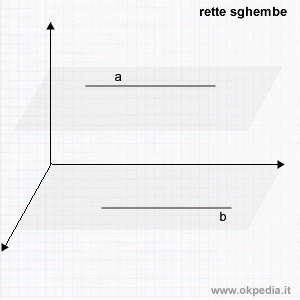
- Quando due rette sono ortogonali? Due rette incidenti sono ortogonali quando dividono il piano in quattro parti uguali.
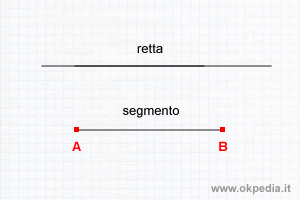
- Qual è la differenza tra retta e segmento? Una retta si prolunga illimitatamente in entrambe le direzioni. Il segmento è delimitato tra due punti, uno iniziale e l'altro finale.
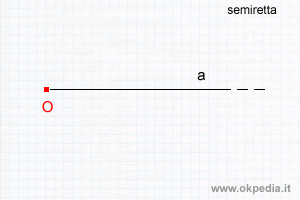
- Cos'è una semiretta? La semiretta è una retta con un punto di origine O.