Algoritmo minimax

L'algoritmo minimax è un algoritmo ricorsivo per la ricerca della mossa migliore in un gioco a somma zero che si svolge tra due giocatori. L'algoritmo minimax è utilizzato nella teoria delle decisioni quando i giocatori si trovano in interazione strategica. È finalizzato a minimizzare la massima perdita possibile di ciascun giocatore. L'algoritmo minimax consente di individuare le scelte migliori dei due giocatori nel corso del gioco, analizzando a ritroso l'albero di gioco a partire dai nodi terminali, ossia dalle possibili situazioni in cui può terminare il gioco ( fine gioco ), e risalendo progressivamente fino alla posizione corrente dei giocatori. Ad esempio nel seguente albero di gioco è rappresentato un gioco sequenziale tra due giocatori, il primo giocatore ( MAX ) deve massimizzare il valore del gioco mentre il secondo giocatore ( MINI ) deve minimizzarlo.

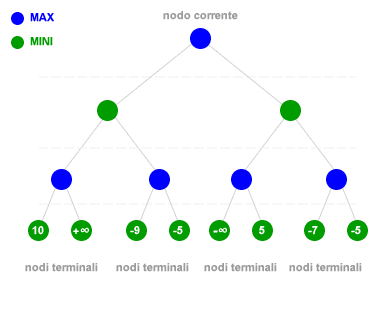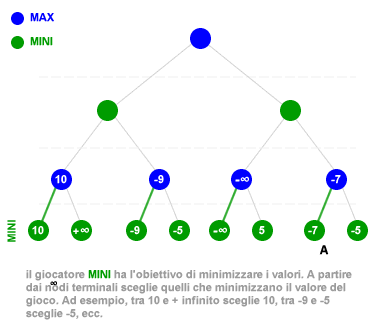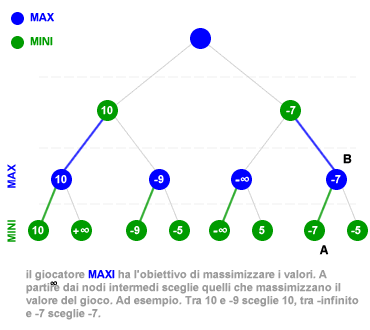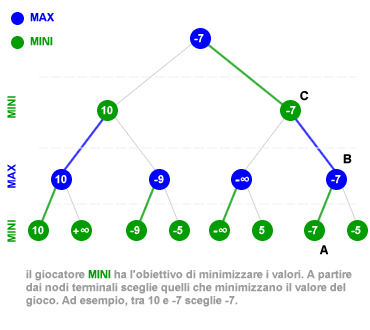
Per comprendere il funzionamento dell'algoritmo proviamo a risalire l'albero di gioco dai nodi terminali alla radice seguendo la logica dell'algoritmo MINIMAX.

• Ultimo livello. Ai nodi terminali è il turno del giocatore MINI, il quale ha l'obiettivo di minimizzare il valore del gioco. Il giocatore MINI individua i valori minimi nei noti terminali e li assegna al nodo genitore. In altri termini, il migliore valore dei nodi viene portato in alto ( backed-up ). Ad esempio, dovendo scegliere tra il nodo che condurrà il gioco a +infinito ( vittoria giocatore MAX ) e quello che condurrà il gioco a +10, il giocatore MINI sceglierà sempre il secondo (+10) poiché minimizza la sua perdita.
• Penultimo livello. Al livello superiore la scelta spetta al giocatore MAX, il quale ha l'obiettivo di massimizzare il valore del gioco. Il giocatore MAX sceglie i nodi con valore maggiore e li riporta sui relativi nodi genitori dell'albero di gioco Ad esempio, tra i nodi 10 e -9 sceglie 10, tra - infinito ( vittoria giocatore MINI ) e -7 sceglie -7. In questo modo il giocatore MAX evita la possibile vittoria del giocatore MINI.
• Primo livello. Al primo livello superiore la scelta spetta nuovamente al giocatore MINI. Tra i nodi 10 e -7 sceglie il nodo -7. Il valore viene riportato sul nodo genitore che, in questo caso, è anche il nodo madre dell'albero logico ( posizione corrente ).

Una volta ricostruito l'albero di gioco a ritroso tramite l'algoritmo MINIMAX è possibile seguire la sequenza delle migliori scelte strategiche del gioco a partire dalla posizione corrente. A partire dal nodo-radice esiste un solo percorso strategico migliore in grado di giungere fino a uno dei nodi terminali dell'albero di gioco. Si tratta del sentiero composto dai nodi A, B e C.

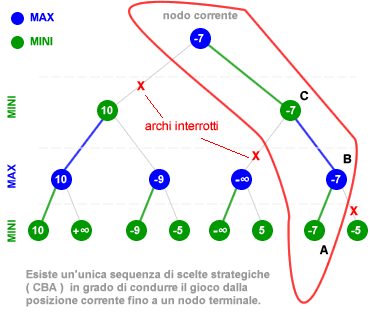
• Prima mossa. Nella posizione corrente al giocatore MINI conviene effettuare la scelta -7 ( nodo C ) poiché gli consente strategicamente di evitare qualsiasi mossa che possa condurre l'altro giocatore alla vittoria ( MAX ). Come si può notare il nodo terminale ( +∞ ) della vittoria di MAX è situato sull'altra ramificazione dell'albero di gioco rispetto alla scelta di MINI.
• Seconda mossa. Nella seconda mossa il gioco passa a MAX. Adesso la posizione corrente è il nodo C sulla ramificazione di destra dell'albero di gioco. MAX ha due possibili scelte dinnanzi, può optare per la scelta che conduce il gioco a -∞ ( vittoria di MINI ) oppure a quella che lo conduce a -7. Essendo un agente razionale, MAX opta per la mossa che conduce il gioco al nodo -7 ( nodo B ) evitando così la vittoria di MINI.
• Terza mossa. Nella successiva mossa è nuovamente il turno di MINI a decidere. La posizione corrente del gioco è il nodo B. Da questa posizione il giocatore MINI può scegliere tra il nodo terminale -7 e -5. Avendo il compito di minimizzare il valore di gioco sceglie il nodo con valore inferiore -7 ( nodo A ) concludendo così il gioco in questa posizione. Il gioco si conclude al nodo terminale A.

L'algoritmo Minimax consente ai due giocatori di minimizzare le rispettive perdite, evitando quelle scelte che conducono a una situazione peggiore o alla vittoria dell'altro giocatore. Il metodo minimax viene dimostrato per la prima volta verso la fine degli anni '20 del Novecento dal matematico e informatico ungherese-statunitense John Von Neumann. È utilizzato per individuare le strategie ottimali nei giochi a somma zero.

Numero finito di stati. L'algoritmo minimax può funzionare soltanto in un gioco con un numero finito di stati. Nel caso di giochi con infiniti stati l'esecuzione dell'algoritmo potrebbe non finire mai ( complessità temporale ).

Complessità algoritmo. Il metodo minimax è una ricerca in profondità in un albero di gioco ( albero di ricerca ) pertanto il numero dei nodi da analizzare cresce in modo esponenziale con la profondità dell'albero. Non sempre è possibile analizzare tutti gli stati possibili di un gioco a partire dai nodi terminali. Ad esempio, soltanto il semplice gioco del tris a nove caselle ha ben oltre 360 mila nodi terminali ( 9! ) ossia combinazioni di gioco, gli scacchi hanno circa 10⁴⁰ nodi terminali, ecc... Al crescere dei nodi terminali cresce la complessità spaziale e la complessità temporale dell'algoritmo. Per ridurre la complessità dell'algoritmo è possibile adottare le tecniche di potatura logica dell'albero di gioco come, ad esempio, la potatura alfa-beta, che consentono di ridurre il numero delle ramificazioni e dei nodi dell'albero di ricerca da analizzare, oppure la tabella delle trasposizioni per eliminare dalla ricerca le sequenze che conducono a un medesimo risultato finale.

Strategie con più di due giocatori. L'algoritmo di ricerca minimax è applicabile nei giochi a due giocatori. Non è altrettanto efficace per interpretare le strategie nei giochi a tre o più giocatori. La presenza di più agenti indipendenti complica notevolmente le scelte strategiche. Ad esempio, due agenti potrebbero stringere degli accordi per eliminare un terzo agente altrimenti più forte individualmente. Gli stessi accordi sono poi basati su criteri quali la lealtà, la reputazione, l'eventuale entità del vantaggio a tradire l'alleato, ecc. La storia e l'economia sono raramente interpretabili tramite la logica della strategia minimax.