Potatura alfa-beta
La potatura alfa-beta è una variante dell'algoritmo minimax che consente di ridurre il numero dei nodi e delle ramificazioni da analizzare per giungere al risultato minimax ottimale. L'idea alla base della potatura alfa-beta è molto semplice e consiste nell'interrompere l'esplorazione in profondità dei nodi quando non sarebbero comunque selezionati dai giocatori perché peggiori rispetto alle alternative possibili. Ciò consente di effettuare una potatura logica dell'albero di gioco e ridurre la complessità dell'algoritmo L'algoritmo minimax è una ricerca in profondità. In altri termini esplode il primo ramo fino al nodo foglia per poi risalire e muoversi verso destra.
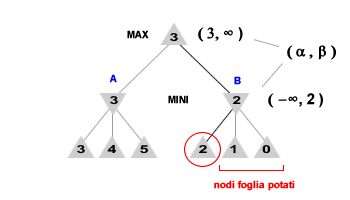
Quando il giocatore massimizzante ( MAX ) incontra un risultato superiore a quelli finora incontrati lo registra nella variabile alfa del nodo. Viceversa, quando il giocatore minimizzante ( MINI ) incontra un risultato inferiore a quelli finora incontrati, ossia migliore dal suo punto di vista, lo registra nella variabile Beta. E così via. L'algoritmo interrompe l'esplorazione di un nodo quando incontra una mossa peggiore rispetto a quelle valutate in precedenza. In tal modo sono eliminate tutte quelle ramificazioni che non sarebbero comunque realizzabili in una situazione di gioco con due giocatori razionali. Il risultato dell'algoritmo minimax con potatura alfa-beta è il medesimo dell'algoritmo minimax completo.
Minore complessità. A differenza dell'algoritmo minimax completo, l'algoritmo con potatura alfa-beta analizza soltanto una parte dell'albero di gioco, giungendo comunque alla medesima soluzione strategica ottimale. Ad esempio, nel grafo precedente l'esplorazione nel nodo B si interrompe non appena l'algoritmo rileva il valore di foglia pari a 2. In questa circostanza l'agente MINI sceglierà un ulteriore valore dei nodi-figli di B tra -∞ e 2. Tuttavia, sappiamo già che l'agente MAX ha un range di scelta tra 3 e ∞. In altri termini, l'agente MAX sceglierà comunque il nodo A poiché vale di più (3) rispetto al massimo valore (2) che potrebbe avere il nodo B. È quindi inutile continuare a esplorare tutte le ramificazioni del nodo B.
In una ramificazione eliminata potrebbe trovarsi anche una soluzione migliore per uno dei due giocatori. Tuttavia, sarebbe una situazione impossibile da raggiungere poiché le scelte strategiche sequenziali dell'altro giocatore ne impedirebbero il percorso. Ad esempio, nel precedente grafo l'agente MINI troverebbe i nodi di valore 1 e 0 subito dopo il nodo 2. Dal punto di vista dell'agente MINI sono nodi migliori del nodo 2. È però un'informazione inutile ai fini della ricerca.
L'efficienza della potatura alfa-beta è fortemente condizionata all'ordine di presentazione dei nodi foglia in una ramificazione. Nell'esempio precedente l'esplorazione del nodo B si è interrotta subito poiché il primo nodo-figlio ha un valore inferiore al range minimo ammissibile. Non è detto però che l'algoritmo sia sempre così fortunato. Proviamo a fare un altro esempio.
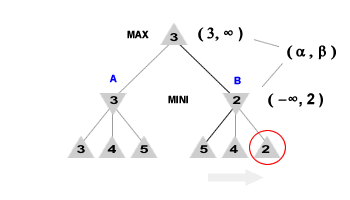
In questo caso l'esplorazione delle ramificazioni del nodo B è comunque completa poiché il nodo con valore inferiore al minimo ammissibile è situato a all'ultimo posto di esplorazione. L'algoritmo minimax è una ricerca in profondità e i nodi di un grafo sono analizzati da sinistra verso destra. L'algoritmo trova dapprima il nodo-figlio di valore 5 ( ammissibile ), poi il nodo-figlio di valore 4 ( ammissibile ) e soltanto alla fine il nodo-figlio di valore 2 ( non ammissibile ). 
Quando la potatura interrompe l'esplorazione, l'algoritmo ha comunque scandagliato l'intero ramificazione del nodo B. Le possibili soluzioni al problema sono un ordinamento dei successori a partire dalla mossa corrente ( potatura alfa-beta con ordinamento ) oppure l'individuazione della mossa migliore mediante una funzione euristica ( potatura alfa-beta euristica ).
