Algoritmo di Dijkstra
L'algoritmo di Dijkstra consente di selezionare gli shortest path ( cammini minimi ) in un grafo ciclico caratterizzato da archi con pesi non negativi. Il cammino minimo è il percorso che permette di unire due nodi distinti del grafo. L'algoritmo è utilizzato nell'ottimizzazione della gestione delle reti idriche, delle reti elettriche e delle reti di trasporto. Ad esempio in una rete elettrica il cammino minimo consente di ridurre la distanza tra il luogo di produzione e quello di consumo dell'energia elettrica, quanto più è breve il percorso tanto minore è la dissipazione dell'energia in calore durante il trasporto. L'algoritmo si basa su due insiemi S e T contenenti rispettivamente i nodi già etichettati e quelli ancora da etichettare.
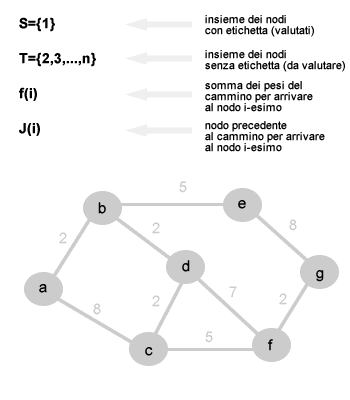
All'inizio dell'esecuzione l'insieme S contiene il nodo di partenza S = { a } e l'insieme T contiene i nodi da analizzare T = { b, c, d, e, f, g }.
- Ciclo 1. Il primo ciclo di esecuzione dell'algoritmo inizia dal nodo di partenza a, a partire dal quale sono analizzati i valori degli archi che congiungono il nodo a con i nodi adiacenti contenuti nell'insieme T ossia il nodo b e il nodo c . A tutti gli altri nodi contenuti nell'insieme T viene assegnato il valore infinito ∞. Analizzando il nodo b e il nodo c otteniamo i seguenti risultati di calcolo:
f(b)=2 // potenziale del nodo b
f(c)=8 // potenziale del nodo c
I due valori sono inferiori ai precedenti valori di f() che, ricordiamo, inizialmente sono posti ad infinito. Essendo inferiori ai precedenti valori si riassegna sia il potenziale dei due nodi e per ciascuno si indica il passo precedente.
f(b)=2 // potenziale del nodo b
j(b)=a // passo precedente
f(c)=8 // potenziale del nodo c
j(c)=a // passo precedente - Ciclo 2. A questo punto l'algoritmo di Dijkstra seleziona il successivo nodo del cammino tra i nodi dell'insieme T { b, c, d, e, f, g } scegliendo quello che minimizza la funzione f(). Tra questi il nodo b ha un potenziale pari a 2, inferiore sia al nodo c (8) che a tutti gli altri nodi (∞). Con la selezione del nodo b quest'ultimo viene spostato dall'insieme T { c, d, e, f, g } all'insieme S { a, b } e si procede ad analizzare i pesi dei nodi dell'insieme T adiacenti al nodo b.
f(d)=2+f(b)=2+2=4 // potenziale del nodo d
f(e)=5+f(b)=5+2=7 // potenziale del nodo e
Anche in questo caso, essendo i due valori f(d) e f(e) inferiori ai precedenti valori delle stesse (infinito) si riassegnano per entrambe indicando il passo precedente.
f(d)=2+f(b)=2+2=4 // potenziale del nodo d
j(d)=b // passo precedente
f(e)=5+f(b)=5+2=7 // potenziale del nodo e
j(e)=b // passo precedente - Ciclo 3. Nel successivo ciclo l'algoritmo ricerca il successivo nodo del cammino tra i nodi dell'insieme T { c, d, e, f, g } scegliendo quello che minimizza la funzione f(). Tra questi il nodo d ha un potenziale pari a 4, inferiore agli altri, e viene pertanto selezionato come passo successivo. Con la selezione il nodo d viene spostato dall'insieme T { c, e, f, g } all'insieme S { a, b, d }. Sono quindi analizzati i pesi sugli archi che congiungono il nodo d ai nodi adiacenti ancora contenuti nell'insieme T ossia il nodo c e il nodo f.
f(c)=2+f(d)=2+4=6 // potenziale del nodo c
f(f)=7+f(d)=7+4=11 // potenziale del nodo f
E' importante notare che il nodo c era già stato valutato in precedenza nel primo di ciclo di esecuzione dell'algoritmo. Il nuovo valore di f(c) è però adesso inferiore (6) a quello già calcolato in precedenza (8). Essendo inferiore si aggiorna anche quest'ultimo valore indicando anche la nuova informazione sul passo precedente.
f(c)=2+f(d)=2+4=6 // potenziale del nodo c
j(c)=d // passo precedente
f(f)=7+f(d)=7+4=11 // potenziale del nodo f
j(f)=d // passo precedente - Ciclo 4. L'algoritmo inizia un nuovo ciclo scegliendo il nodo successivo del cammino con potenziale inferiore tra quelli contenuti nell'insieme T. Il nodo c ha un valore potenziale pari a 6, inferiore a tutti gli altri, e viene selezionato come passo successivo. Con la selezione il nodo c viene spostato dall'insieme T { e, f, g } all'insieme S { a, b, c, d }. Sono quindi analizzati i pesi sugli archi che congiungono il nodo c ai nodi adiacenti ancora contenuti nell'insieme T ossia il nodo f .
f(f)=5+f(c)=5+6=11 // potenziale del nodo f
Anche in questo caso il nodo f era già stato valutato in precedenza ma il nuovo valore (11) non è inferiore a quello già assegnato (11) quindi non si procede a riassegnare un nuovo potenziale al nodo f. - Ciclo 5. L'algoritmo seleziona il nodo con potenziale inferiore all'interno dell'insieme T { e, f, g } ossia il nodo e (7) e lo sposta dall'insieme T { f, g } all'insieme S { a, b, c, d, e }. A partire dal nodo e analizza i pesi sugli archi che lo congiungono ai nodi dell'insieme T.
f(g)=8+f(e)=8+7=15 // potenziale del nodo g
Essendo f(g) inferiore al suo valore precedente (∞) viene modificato con il nuovo valore (15) e viene modificata l'informazione sul passo precedente del nodo g ossia j(g)=e. - Ciclo 6. L'algoritmo seleziona il nodo con potenziale inferiore all'interno dell'insieme T { f, g } ossia il nodo f (11) e lo sposta dall'insieme T { g } all'insieme S { a, b, c, d, e, f }. A partire dal nodo f analizza i pesi sugli archi che lo congiungono ai nodi dell'insieme T.
f(g)=2+f(f)=2+11=13 // potenziale del nodo g
Essendo f(g) inferiore al suo valore precedente (15) viene modificato con il nuovo valore (13) e viene modificata anche l'informazione sul passo precedente del nodo g ossia j(g)=f. - Ciclo 7. L'algoritmo seleziona il nodo con potenziale inferiore all'interno dell'insieme T { g } ossia il nodo g (13) e lo sposta dall'insieme T { } all'insieme S { a, b, c, d, e, f, g }. A partire dal nodo g analizza i pesi sugli archi che lo congiungono ai nodi dell'insieme T ma non esiste più alcun nodo adiacente nell'insieme T.
- Ciclo 8. Non essendoci più alcun nodo nell'insieme T l'algoritmo si interrompe.
Al termine dell'esecuzione l'algoritmo ha costruito una serie di valori che consentono di individuare il cammino più veloce (o meno costoso) da qualsiasi nodo della rete al nodo di partenza (a). E' sufficiente seguire a ritroso il cammino seguendo l'informazione contenuta nella variabile J() del nodo di destinazione.
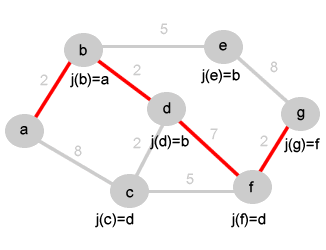
Seguendo l'informazione sul passo precedente contenuta nella variabile J(g) nel nodo finale si individua il passo precedente f. Sul nodo f si individua il passo precedente leggendo l'informazione J(f) del nodo f e via dicendo fino a giungere al nodo di partenza (a). L'algoritmo di Dijkstra ha individuato il percorso meno costoso.
