Tabella delle trasposizioni

La tabella delle trasposizioni contiene le diverse permutazioni di elementi che conducono a un medesimo risultati. È utilizzata negli algoritmi di esplorazione e di ricerca degli alberi di gioco per evitare di analizzare i diversi cammini ( sequenza di mosse ) che portano a un medesimo stato. Ad esempio, nel seguente albero di gioco sono rappresentate sequenze diverse, due di queste portano al medesimo risultato ( A-C-E = B-D-H ) e altre due ( A-C-F e B-D-G ) sono tra loro simmetriche.

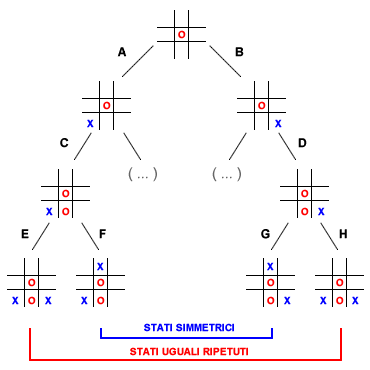
La tabella delle trasposizioni consente di effettuare una potatura logica dell'albero di gioco ( albero di ricerca ). In tal modo l'algoritmo di ricerca evita di analizzare più volte gli stati ripetuti, riducendo i tempi di ricerca dello stato migliore e la complessità di calcolo dell'algoritmo È inutile analizzare tutte le diverse sequenze che conducono a un medesimo risultato fallimentare. Una volta assodato che uno stato finale è fallimentare, lo sono anche tutte le altre combinazioni di scelte che conducono allo stesso risultato finale. In alcuni casi, come nel gioco del tris, gli stati simmetrici non sono altro che stati ripetuti riflessi in orizzontale. È quindi possibile eliminare dalla ricerca, oltre agli stati uguali, anche gli stati simmetrici.