Algoritmo con taglio probabilistico
Un algoritmo con taglio probabilistico è una tipologia di algoritmo di ricerca con taglio in avanti. Nel corso dell'elaborazione l'algoritmo matura una esperienza che gli consente di effettuare un taglio in avanti quando incontra situazioni simili a quelle già analizzate in passato. L'algoritmo memorizza in un database l'associazione tra le varie combinazioni di cammino all'interno di un albero di ricerca e le probabilità di successo riscontrate. In tal modo, l'algoritmo può effettuare una potatura logica sui nodi futuri che presentano situazioni simili, senza doverli scandagliare in profondità ( taglio probabilistico). Ad esempio, nel seguente albero di ricerca l'algoritmo può giungere a situazioni positive W ( Win ) e negative L ( Lost ).
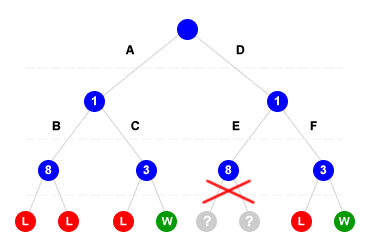
L'algoritmo con taglio probabilistico inizia ad analizzare in profondità l'albero di ricerca da sinistra a destra. Inizialmente l'algoritmo non ha alcuna esperienza. La prima ricerca in profondità consiste nello scandagliare il ramo A+B (1+8) che conduce a due sconfitte ( L ). La seconda ricerca analizza il ramo A+C (1+3) che conduce a una sconfitta ( L ) e a una vittoria ( W ). Nel terzo caso l'algoritmo analizza il ramo D+E (1+8) che, nel nostro semplice esempio, è uguale al cammino A+B. Sulla base dell'esperienza maturata l'algoritmo può calcolare una probabilità di insuccesso pari al 100% ( due sconfitte su due in A+B ) ed evitare di scandagliare anche le sotto-ramificazioni del cammino D+E ( taglio di ricerca ). L'algoritmo passa direttamente ad analizzare il successivo cammino D+F.
Taglio probabilistico ponderato alla probabilità di successo. Nell'esempio precedente il taglio probabilistico si basa soltanto su un caso empirico (A+B). Si tratta ovviamente di una situazione volutamente semplificata per esporre meglio il concetto di taglio probabilistico. Nella realtà, il taglio probabilistico si basa su una grande quantità di dati ( esperienza ) e raramente ci si trova dinnanzi a una probabilità di insuccesso del 100%. Molto più frequentemente il taglio della ricerca si basa su una decisione casuale ponderata alla probabilità di successo attesa. Ad esempio, se un cammino ha l'80% di condurre a una sconfitta, otto volte su dieci viene tagliato dall'algoritmo di ricerca e due volte su dieci viene, invece, scandagliato fino in profondità. In questo modo l'algoritmo continua a maturare esperienza, rettificando e migliorando quella passata. E così via.
Complessità spaziale e temporale. L'algoritmo con taglio probabilistico è penalizzato dalla necessità di dover maturare esperienza in molti cicli di elaborazione ( complessità temporale ) prima di diventare efficace. A questo problema se ne aggiunge anche un altro, forse anche peggiore. L'esperienza maturata deve essere fisicamente registrata in un database con un conseguente problema di spazio di memoria disponibile ( complessità spaziale ). Potrebbero non esistere supporti di memoria hardware sufficientemente grandi per contenere tutta l'esperienza maturata dall'algoritmo. Il problema della complessità spaziale è già ben noto nell'approccio all'intelligenza artificiale basato sulle tabelle ( tabelle intelligenza artificiale ).
