Grafo di pianificazione

Un grafo di pianificazione ( planning graph ) è una rappresentazione grafica dello spazio degli stati e delle azioni che collegano gli stati. È un grafo orientato in cui ogni nodo rappresenta un fluente S_t ossia uno stato (S) in un particolare istante temporale (t) oppure un'azione. Le azioni e gli stati sono rappresentate in modo diverso, ad esempio le azioni sono sottolineate o cerchiate. Il grafo di pianificazione è caratterizzato dalla suddivisione in livelli. A partire da uno nodo iniziale S₀ sono analizzate tutte le azioni applicabili ( es. A₀ ). Un'azione è applicabile in uno stato fluente Si se tutte le sue precondizioni sono soddisfatte. Ogni azione ammissibile genera, a sua volta, nuovi stati fluenti ( es. S₁ ) nel livello successivo del grafo di pianificazione. In un grafo di pianificazione ogni azione A_j ( azione al livello j del grafo ) è connessa alle sue precondizioni S_j e ai suoi effetti S_j+1. La rappresentazione dei livelli del grafo di pianificazione può essere orientata in verticale o in orizzontale. La seguente rappresentazione mostra un esempio di grafo di pianificazione verticale.

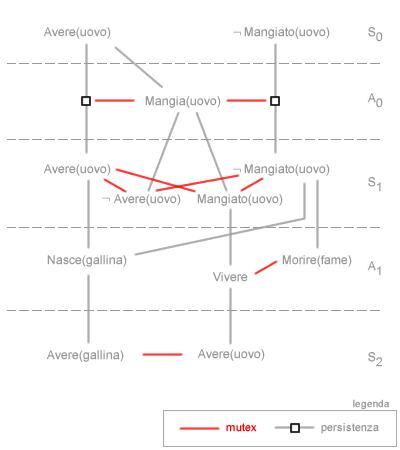
Nel grafo di pianificazione gli stati possono persistere nel livello successivo. La persistenza dello stato è indicata con un apposito simbolo grafico ( quadrato nero ) e sono dette azioni di persistenza o no-op. Alcune azioni e stati possono, invece, escludersi mutevolmente, queste situazioni sono dette mutex ( mutua esclusione ) e sono rappresentate da collegamenti differenti ( es. collegamenti di colore rosso ). La rappresentazione del grafo di pianificazione termina quando due livelli consecutivi sono identifici ( livellamento ) e nessun'altra azione può apportare variazioni allo spazio degli stati nel livello successivo. I grafi di pianificazione agevolano la ricerca da uno stato iniziale a uno stato obiettivo e la costruzione delle euristiche di ricerca.

---

• Complessità polinomiale. Il grafo di pianificazione può essere utilizzato nei problemi proposizionali. È invece complesso utilizzarlo per rappresentare tutti i valori che possono assumere le variabili di un problema nella logica del primo ordine. Dato un problema con n_l letterali, n_a azioni e n livelli, la complessità del grafo di pianificazione ha una dimensione pari a O(n(n_a+n_l)²).
• Mutua esclusione ( Mutex ). La relazione di mutua esclusione si verifica quando uno stato esclude il verificarsi contemporaneo di un altro stato/azione oppure quando un'azione esclude un'altra azione o uno stato nello stesso tempo ( livello ). Ad esempio, lo stato Avere(uovo) esclude la sua negazione ¬Avere(uovo). Allo stesso modo l'azione Mangia(uovo) esclude lo stato Avere(uovo) e ¬Mangiato(uovo). Quando due azioni negano l'effetto l'una dell'altra, queste non possono essere scelte contemporeamente in uno stesso livello poiché generano effetti inconsistenti. Un'azione potrebbe anche generare degli effetti che negano le precondizioni di un'altra azione, interferendo con l'esistenza stessa dei letterali e modificando l'insieme delle azioni applicabili ( possibili ) in un determinato livello. A volte le azioni potrebbero escludersi a vicenda anche perché hanno la medesima precondizione. Ad esempio, la precondizione Avere(uovo) è la stessa sia per Nasce(gallina) e per Mangia(uovo) ma un'azione esclude il verificarsi dell'altra ( condizione di esclusività ).
• Soddisfacibilità. L'ultimo livello degli stati del grafo di pianificazione consente di verificare la soddisfacibilità o meno di un obiettivo. Se il letterale obiettivo è presente negli stati dell'ultimo livello del grafo, allora il problema è soddisfacibile. In questo caso, per ottenere il percorso delle azioni da intraprendere a partire da uno stato iniziale S₀, è sufficiente percorrere all'indietro tutte le azioni e gli stati dei livelli dallo stato obiettivo S_n. Viceversa, se il letterale obiettivo non è presente negli stati dell'ultimo livello del grafo di pianificazione S_n, allora il problema non ha una soluzione.
  
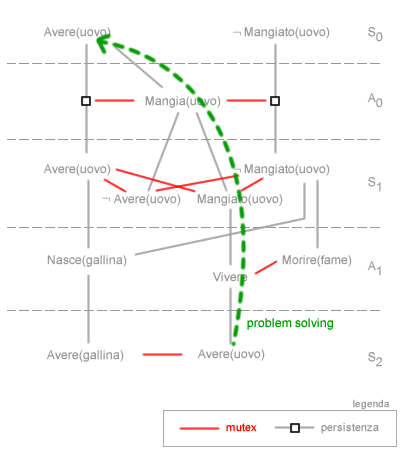
• Non completezza della ricerca. L'assenza dell'obiettivo nello spazio degli stati consente di affermare con certezza che un problema è irrisolvibile. Non è però possibile affermare con altrettanta certezza che la presenza di un letterale obiettivo nello spazio degli stati implica una soluzione al problema. La mera presenza dell'obiettivo nello spazio degli stati non assicura l'esistenza di una soluzione. Per appurare l'esistenza di una soluzione è necessario verificare l'esistenza di un collegamento logico ( pianificazione ) tra lo stato obiettivo e lo stato iniziale.
• Costo della soluzione. Il numero dei livelli del grafo fornisce una stima del costo della soluzione per raggiungere un obiettivo ( euristica della somma dei livelli ). Ad esempio, l'obiettivo Avere(gallina) ha un costo pari a due poiché compare nel secondo livello dello spazio degli stati (S₂). L'obiettivo Mangiato(uovo), invece, ha un costo pari a uno poiché compare nel primo livello dello spazio degli stati (S₁). L'obiettivo Avere(uovo), infine, ha un costo pari a zero poiché è già presente nello spazio degli stati iniziali (S₀). Il costo della soluzione è pari al numero dei livelli necessari per giungere da un determinato stato iniziale (S_i) al primo stato (S_n) in cui compare il letterale obiettivo.
  • Serializzazione del grafo di pianificazione. L'euristica della somma dei livelli conta soltanto i livelli ma ogni livello potrebbe avere migliaia di azioni ammissibili, rendendo poco verosimile la stima della complessità computazionale della ricerca. Per risolvere questo problema è consigliabile eseguire soltanto un'azione per ogni livello temporale del grafo di pianificazione. In questo modo si ottiene una pianificazione seriale e l'euristica fornisce una stima attendibile del costo della soluzione e del percorso necessario per raggiungerla.
  • Obiettivi congiunti. Nel caso degli obiettivi congiunti l'euristica della somma dei livelli potrebbe essere poco attendibile. Ad esempio, la congiunzione di letterali Avere(gallina) ∧ Avere(uovo) viene raggiunta al secondo livello. Il problema sembrerebbe risolvibile con una complessità pari a due. In realtà questa stima è errata in quanto l'obiettivo congiuntivo è irrisolvibile. Nel secondo livello i due letterali sono legati tra loro da una relazione di mutua esclusione ( mutex ) e, pertanto, non possono verificarsi contemporaneamente. In conclusione, l'euristica della somma dei livelli è attendibile soltanto quando i letterali congiuntivi appaiono in uno stesso livello e non è presente alcuna relazione di mutua esclusione tra i letterali congiuntivi.
• Vincoli indiretti. Il grafo di pianificazione è efficace se il problema può essere trasformato in un insieme di sottoproblemi indipendenti, ognuno dei quali non influisce sulla soluzione degli altri. In caso contrario diventa difficoltoso trovare un'euristica in grado di affermare la soddisfacibilità o meno di un obiettivo senza tenere in conto tutti i vincoli del problema. Ad esempio, se il problema consiste nel porre dei cubi uno sopra l'altro, è possibile effettuare dei controlli di mutua esclusione tra due cubi. Ad esempio, quando il cubo A è sul cubo B, è impossibile porre il cubo B sul cubo A. Successivamente è possibile porre il cubo B sul cubo C, escludendo l'ipotesi contraria ( C su B ). A questo punto l'algoritmo può verificare se è possibile porre il cubo C sul cubo A e, non trovando alcun vincolo, lo ritiene erroneamente possibile.
  
  
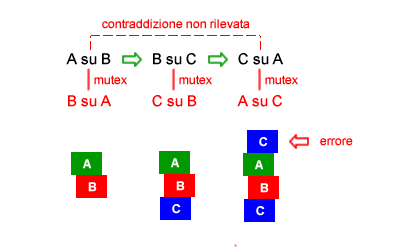
  Questo errore si verifica perché l'algoritmo controlla soltanto le relazioni mutex tra le singole coppie dei cubi senza tenere in conto le relazioni tra un cubo e tutti gli altri cubi. In questo caso il problema è stato scomposto da un problema a tre elementi in tre sottoproblemi da due elementi ma questi ultimi non sono completamente indipendenti gli uni dagli altri. Questo errore potrebbe essere evitato esplorando la pianificazione, tenendo in considerazione anche le scelte passate e i vincoli non diretti, ossia i vincoli derivati dalle triangolazioni degli elementi.
• Ricerca in avanti. Il grafo di pianificazione può essere utilizzato anche nella ricerca in avanti. Dato una situazione iniziale S0 e un obiettivo da raggiungere, l'algoritmo ricerca in profondità le combinazioni di azioni. La ricerca termina quando l'esplorazione conduce alla prima soluzione accettabile del problema ( es. "avere un uovo in futuro" ). L'algoritmo consuma una minore quantità di memoria rispetto alla ricerca all'indietro poiché non deve preventivamente esplodere l'intero grafo di pianificazione prima di iniziare il processo di ricerca. E' sufficiente applicare la serializzazione delle scelte in profondità. L'algoritmo interrompe la ricerca in una ramificazione quando incontra un vicolo cieco o una contraddizione, per passare alla ramificazione successiva.
  
  
  
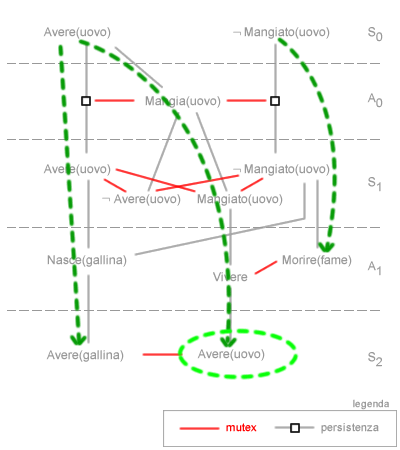
  Una volta trovata la soluzione è completa, in quanto sono già stato analizzati tutti i vincoli del percorso. Non è detto però che la soluzione trovata con la ricerca in avanti sia anche ottimale. Per giungere alla soluzione ottimale l'algoritmo non deve concludere il processo di ricerca quando trova la prima soluzione accettabile al problema, bensì deve continuare a scandagliare tutte le possibili combinazioni del grafo di pianificazione. La soluzione ( cammino ) con minore costo tra tutte quelle trovate è la soluzione ottimale al problema. Questa ricerca implica un maggiore consumo di tempo di esecuzione.