Pianificazione lineare
Una pianificazione lineare è una sequenza di azioni che consente di raggiungere un obiettivo a partire da una situazione iniziale. Una pianificazione lineare è totalmente ordinata in quanto le azioni del piano devono essere eseguite esattamente nell'ordine previsto.
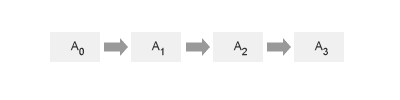
In una sequenza di azioni possono presentarsi dei sottoproblemi indipendenti. In tali circostanze la commutazione dell'ordine di esecuzione di alcune azioni, o di sotto-sequenze di azioni, potrebbe essere equivalente. Tali situazioni sono risolte con maggiore efficienza dalle pianificazioni parzialmente ordinate. Ad esempio, nel seguente caso è indifferente l'ordine di esecuzione delle azioni A1 e A2.
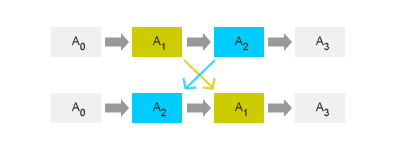
In questi casi la pianificazione lineare non rappresenta adeguatamente le possibilità di azione. La pianificazione parzialmente ordinata, invece, consente una rappresentazione può efficace. Seguendo il seguente schema l'agente può scegliere indifferentemente di compiere prima l'azione A1 o l'azione A2.
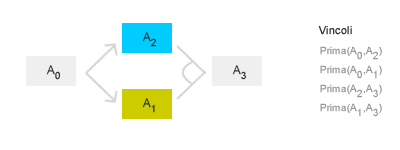
La pianifiazione si dice parzialmente ordinata in quanto l'agente deve rispettare l'ordine di esecuzione delle azioni soltanto nel caso della prima azione A0 e dell'ultima azione A3. È invece indifferente l'ordine di esecuzione di A1 e A2. L'insieme delle sequenze di azioni possibili ( piani ) è detto spazio dei piani.
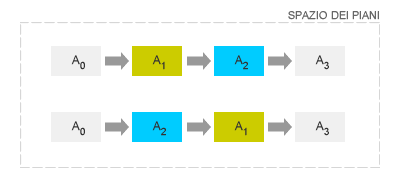
Una pianificazione parzialmente ordinata consente di rappresentare la pianificazione tramite un insieme di vincoli e un insieme di azioni. A partire da un obiettivo finale, l'algoritmo avvia una ricerca nello spazio dei piani per trovare le azioni più vicine all'obiettivo, attuando una regressione progressiva sulle azioni precedenti ( precondizioni ) fino a ricostruire l'intero piano. Ad esempio, in un automobile il piano per la sostituzione della ruota bucata con la ruota di scorta può essere ricostruito nel seguente modo:
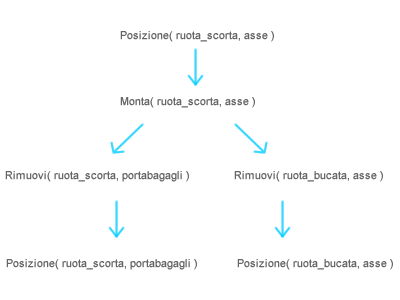
A partire dall'obiettivo finale, Posizione( ruota_scorta, asse ), l'algoritmo risale alle sue precondizioni scoprendo che è necessario aver montato la ruota di scorta Monta( ruota_scorta, asse ). Andando più a ritorso, l'algoritmo scopre che per montare la ruota di scorta è necessario aver rimosso la ruota bucata dall'asse, Rimuovi( ruota_bucata, asse ), e aver rimosso la ruota di scorta dal portabagagli, Rimuovi( ruota_scorta, portabagagli ). L'algoritmopuò, infine, risalire alle precondizioni di queste ultime due azioni, scoprendo che la sequenza di azioni è possibile quando la ruota sull'asse è bucata e la ruota di scorta è nel portabagli.
- Sottoproblemi. La complessità computazionale della pianificazione si riduce quando il problema può essere suddiviso, parzialmente o completamente, in due o più sottoproblemi. Ad esempio, la sequenza di rimozione della ruota di scorta dal portabagagli e di rimozione della ruota bucata dall'asse possono essere considerati due sottoproblemi indipendenti.
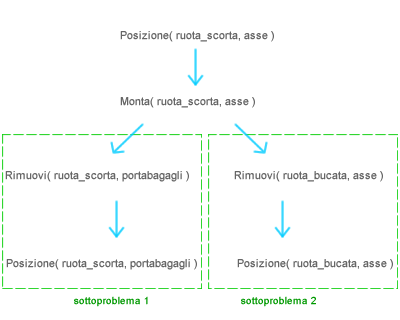
Considerare le sequenze di azioni come sottoproblemi consente di ridurre notevolmente la ricerca nello spazio dei piani. Un problema viene suddiviso in sottoproblemi e ciascun sottoproblema è risolto separatamente dagli altri. Ogni sottoproblema ha un numero di variabili inferiore rispetto al problema complessivo. La somma delle combinazioni delle variabili di tutti i sottoproblemi è, quindi, inferiore alla combinazione di tutte le variabili del problema completo. - Sottoproblemi indipendenti. L'organizzazione del problema in sottoproblemi è efficace soltanto quando i sottoproblemi sono indipendenti. Quando le azioni dei sottoproblemi si influenzano vicendevolmente, un'azione posta in essere per risolvere un sottoproblema ( sotto-obiettivo ) potrebbe invalidare l'obiettivo già raggiunto in un altro sottoproblema.
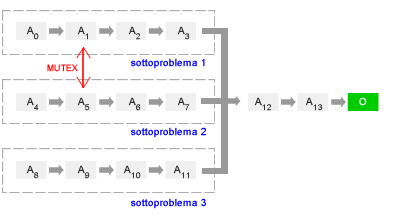
Quando le azioni dei sottoproblemi si influenzano, i sotto-obiettivi dei sottoproblemi non sono serializzabili. È quindi necessario imporre un'ulteriore regola, qualsiasi azioni non deve invalidare i sotto-obiettivi già raggiunti. Tuttavia, imponendo questa regola, l'ordine di risoluzione dei sotto-obiettivi può influenzare sensibilmente lo spazio dei piani. Il problema può essere analizzato come un problema di vincoli CSP.
