Scatola di Edgeworth

La scatola di Edgeworth è uno strumento grafico per analizzare la distribuzione e lo scambio delle quantità di due beni tra due soggetti economici e le condizioni di equilibrio in un'economia di puro scambio. Lo strumento viene ideato dall'economista britannico Francis Ysidro Edgeworth e perfezionato da A.L. Bowley. La scatola di Edgeworth può essere utilizzata sia per analizzare lo scambio delle quantità di due beni ( X e Y ) tra due soggetti economici in un'economia di puro scambio ( scatola degli scambi di Edgeworth ) e sia per analizzare l'allocazione dei fattori produttivi ( K, L ) tra due produzioni di due imprese. Nel primo caso si utilizzano le curve di indifferenza tra i due beni economici, mentre nel secondo caso si utilizzano le curve di isoquanto tra i due fattori produttivi.

Scatola degli scambi di Edgeworth. Dati due soggetti economici ( A e B ) con due dotazioni di beni economici ( X e Y ), senza attività di produzione, la scatola di Edgeworth permette di determinare la quantità di scambio del bene tra i due soggetti, sulla base delle loro dotazioni e delle preferenze individuali.

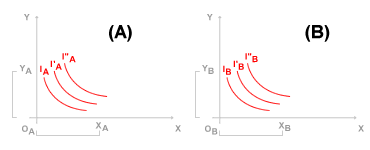
Nel primo diagramma cartesiano ( diagramma A ) è rappresentata la famiglia delle curve di indifferenza del soggetto A. Il soggetto A ha una dotazione iniziale di X_A quantità del bene X e una dotazione di Y_A quantità del bene Y. Nel secondo diagramma cartesiano ( diagramma B ) è rappresentata la famiglia delle curve di indifferenza del soggetto B. Il soggetto B ha una dotazione iniziale di X_B quantità del bene X e una dotazione di Y_B quantità del bene Y. Per realizzare la scatola di Edgeworth ( costruzione della scatola di Edgeworth ) è sufficiente ruotare di 180° il diagramma cartesiano del soggetto B ( diagramma B ) e sovrapporlo al diagramma cartesiano del soggetto A ( diagramma A ). Il risultato finale è un doppio grafico a forma di rettangolo con due origini. A partire dall'origine in basso a sinistra O_A è possibile misurare la dotazione e le quantità di scambio dei beni del soggetto A. A partire dall'origine in alto a destra O_B, viceversa, quelle del soggetto B. La scatola di Edgeworth si presenta graficamente nel seguente modo:

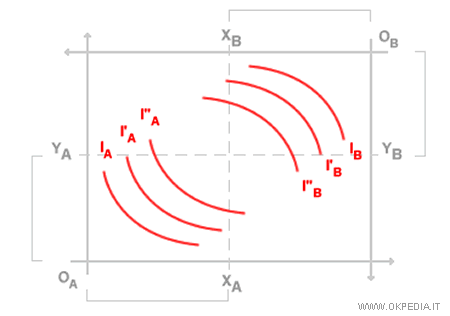
La scatola di Edgeworth è composta da un doppio diagramma cartesiano. Entrambi i diagrammi misurano sugli assi le quantità del bene A e del bene B. La misura degli assi X e Y della scatola di Edgeworth è determinata dalla somma delle dotazioni dei beni dei due soggetti economici. Ad esempio, l'asse delle ascisse della scatola è determinata dalla somma X_A + X_B della quantità del bene X in dotazione del soggetto A e del soggetto B. Allo stesso modo, l'asse delle ordinate della scatola è determinata dalla somma Y_A + Y_B della quantità del bene Y in dotazione del soggetto A e del soggetto B. Le curve di indifferenza restano convesse verso il rispettivo punto di origine. Ad esempio, la famiglia di curve di indifferenza I_B sono convesse rispetto all'origine O_B. Il soggetto B preferisce sempre la curva di indifferenza I"_B ( più esterna da O_B ) alla curva di indifferenza I'_B. Questa particolare caratteristica della scatola di Edgeworth consente di misurare le variazioni nelle dotazioni dei beni dei due soggetti economici durante lo scambio. La scatola di Edgworth è uno degli strumenti grafici dell'economia politica ( microeconomia ).

Scatola della produzione di Edgeworth. Nella scatola di Edgeworth per la produzione sugli assi cartesiani sono rappresentate le quantità dei fattori produttivi K e L. Gli isoquanti mostrano sul piano cartesiano le combinazioni dei fattori per la produzione dei beni A e B. La somma K_A+K_B è pari alla quantità complessiva di capitale ( K ) sul mercato, mentre la somma L_A+L_B è pari alla quantità complessiva di lavoro ( L ) nel mercato. Sulla base della tecnologia adottata dalle imprese ( isoquanti ) per la produzione dei due beni ( A, B ), i punti di tangenza tra le curve di isoquanto determinano le allocazioni ottimali del capitale ( K ) e del lavoro ( L ).

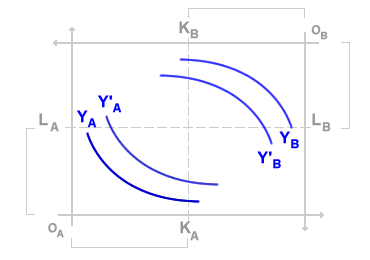
Equilibrio della scatola di Edgeworth. L'equilibrio nella scatola di Edgeworth si verifica nei punti di tangenza tra le curve di indifferenza dei due consumatori ( punto di contratto ). In tali punti, il saggio marginale di sostituzione tra i beni è uguale per entrambi i consumatori. L'equilibrio nella scatola di Edgeworth è una situazione di ottimo paretiano poiché, in un punto di tangenza tra le curve di indifferenza, nessun consumatore può migliorare la propria utilità senza peggiorare quella dell'altro consumatore. L'insieme dei punti di tangenza delle curve di indifferenza è detto curva dei contratti. Allo stesso modo, si dice curva dei contratti anche l'insieme dei punti di tangenza delle curve di isoquanto.