Ricerca hill climbing
La ricerca hill climbing è una ricerca locale basata su un ciclo di ricerca di nodi con valori più alti ( migliori ) nei pressi di un particolare nodo di riferimento. Il termine hill climbing indica la capacità dell'algoritmo di "scalare" i nodi verso quelli con valori maggiori. Lo spazio di ricerca dell'algoritmo hill climbing è limitato ai soli nodi vicini a quello corrente. Quando un nodo vicino è migliore del nodo di riferimento ( nodo corrente ), quest'ultimo viene sostituito con il nuovo nodo. Il ciclo di elaborazione dell'algoritmo hill climbing termina quando viene raggiunto il nodo con valore più alto ( "picco" ) ossia quando nessun nodo vicino ha valore superiore a quello di riferimento. Ad esempio poniamo di avere la seguente matrice con 100 nodi e di avere l'obiettivo di raggiungere il nodo con valore più alto. Una ricerca sequenziale implicherebbe 100 passi nel peggiore dei casi e 50 passi in media per trovare il nodo con valore più alto.
Nel caso della ricerca locale scegliamo un nodo di riferimento iniziale, in base a una funzione euristica ( ricerca informata ) oppure a caso, e procediamo con l'elaborazione della ricerca locale. In 5 passi l'algoritmo raggiunge l'obiettivo. L'esempio è volutamente banale per rendere meglio l'idea del funzionamento di una ricerca hill climbing. Tuttavia, in un algoritmo hill climbing la probabilità di fallire la ricerca è molto elevata. L'algoritmo hill climbing ha i seguenti vantaggi e svantaggi.
Minore complessità. L'algoritmo hill climbing utilizza poca quantità di memoria (complessità spaziale). Non dovendo analizzare tutti i nodi e i cammini possibili è caratterizzato da minori tempi di elaborazione (complessità temporale). È quindi un algoritmo molto rapido e veloce.
Massimo locale. Uno dei principali handicap dell'algoritmo hill climbing è il rischio di incappare in un massimo locale. Quando l'algoritmo trova un valore massimo locale, maggiore rispetto a tutti i nodi vicini, si blocca. Tuttavia, ciò non esclude la presenza lontana di massimi globali con valore superiore. La ricerca hill climbing ha gli stessi svantaggi della ricerca greedy ( ricerca golosa ). Si muove rapidamente verso il nodo migliore utilizzando una strategia troppo miope. Per tale ragione è conosciuta anche come ricerca locale greedy. Nell'esempio precedente se l'algoritmo avesse iniziato la ricerca locale da un nodo iniziale diverso sarebbe potuto incappare in un massimo locale sub-ottimale.
Per ridurre questo rischio è possibile ricorrere a diverse tecniche. In primo luogo si può cercare di migliorare la funzione euristica di individuazione dei nodi iniziali. In secondo luogo è consigliabile eseguire più volte l'algoritmo di ricerca locale seguendo la logica dell'algoritmo hill climbing iterativo. Elaborando più volte l'algoritmo hill climbing da nodi iniziali differenti, tenendo in memoria il migliore risultato ottenuto, è possibile migliorare l'efficacia della ricerca senza penalizzare eccessivamente la velocità e il tempo di elaborazione dell'algoritmo hill climbing. Un'altra tecnica computazionale per ridurre il rischio del massimo locale sub-ottinale è l'algoritmo hill climbing stocastico in cui la scelta del nodo successore è determinata casualmente da una funzione stocastica e non è sempre quella migliore possibile.
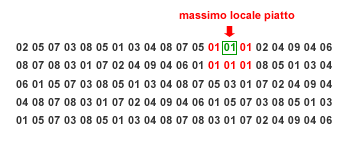
Massimo locale piatto. Un altro rischio dell'algoritmo hill climbing è quello di imbattersi in un massimo locale piatto. Quando tutti i nodi vicini hanno un valore uguale al nodo corrente l'algoritmo si blocca. Nel seguente esempio il nodo corrente non prosegue l'esplorazione dal nodo corrente ( valore 01 ) nonostante siano presenti almeno cinque cammini diversi per arrivare fino al massimo globale ( valore 09 ) a partire dai nodi vicini di pari valore.
Per ridurre il rischio di imbattersi in un massimo locale piatto è, invece, possibile ammettere una percentuale di spostamenti laterali tra nodi vicini a parità di valore ( mossa laterale ) per esplorare lo spazio di ricerca locale quando non siano presenti nelle vicinanze altri nodi con valori superiori a quello corrente. È sconsigliabile consentire sempre gli spostamenti laterali in quanto potrebbe generare un ciclo infinito ( loop ) nell'elaborazione dell'algoritmo.
