Hill climbing stocastico
L'algoritmo hill climbing stocastico è una particolare variante dell'algoritmo di ricerca locale hill climbing in cui la selezione del nodo successore da esplorare è determinata da una variabile casuale ( esplorazione randomizzata ). Una funzione stocastica estrapola uno dei nodi vicini da analizzare e lo seleziona soltanto se quest'ultimo ha un valore migliore rispetto al nodo corrente. La scelta del nodo da analizzare può essere determinata nei seguenti modi:
- Numero casuale con uguale probabilità per tutti i nodi. La funzione stocastica estrapola un numero casuale attribuendo a ogni nodo vicino la stessa probabilità di essere estratto.
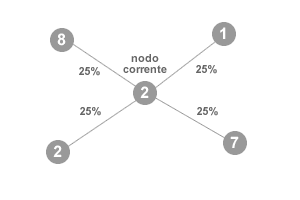
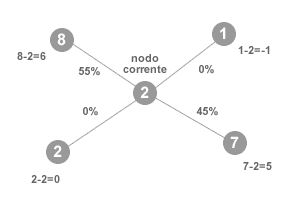
- Numero casuale con diversa probabilità tra i nodi. La funzione stocastica estrapola un numero casuale attribuendo a ogni nodo una differente probabilità di essere estratto. Ad esempio, la probabilità di ogni nodo può essere determinata dalla differenza positiva tra il valore del nodo e quello del nodo corrente. In tal modo i nodi con valore maggiore hanno una probabilità maggiore d'essere estratti mentre quelli con valore inferiore al nodo corrente sono esclusi dall'estrazione (probabilità zero). Questa versione è leggermente più veloce rispetto a quella con eguale probabilità di scelta dei nodi.
La scelta casuale dell'algoritmo hill climbing stocastico consente di ottenere diversi vantaggi rispetto a un algoritmo hill climbing trazionale.
 Maggiore completezza. La scelta casuale consente di analizzare cammini secondari altrimenti esclusi dall'algoritmo hill climbing tradizionale. Ad esempio, tra i nodi vicini con valore superiore a quello corrente potrebbe esserci un nodo di valore più alto che conduce a una soluzione sub-ottimale e un nodo di valore più basso che, invece, conduce a una soluzione ottimale. L'algoritmo hill climbing tradizionale non riuscirebbe mai ad esplorare il cammino ottimale poiché ha un'orizzonte di analisi molto limitato, si limita a scegliere il nodo vicino con valore maggiore, senza analizzare gli effetti nella mossa successiva. L'algoritmo hill climbing stocastico, invece, non esclude a priori le seconde scelte ed esplora un maggior numero di cammini possibili.
Maggiore completezza. La scelta casuale consente di analizzare cammini secondari altrimenti esclusi dall'algoritmo hill climbing tradizionale. Ad esempio, tra i nodi vicini con valore superiore a quello corrente potrebbe esserci un nodo di valore più alto che conduce a una soluzione sub-ottimale e un nodo di valore più basso che, invece, conduce a una soluzione ottimale. L'algoritmo hill climbing tradizionale non riuscirebbe mai ad esplorare il cammino ottimale poiché ha un'orizzonte di analisi molto limitato, si limita a scegliere il nodo vicino con valore maggiore, senza analizzare gli effetti nella mossa successiva. L'algoritmo hill climbing stocastico, invece, non esclude a priori le seconde scelte ed esplora un maggior numero di cammini possibili.

Ad esempio, a partire dal nodo iniziale 02 l'algoritmo hill climbing tradizionale sceglierebbe sempre il nodo con valore 08 (scelta primaria) ottenendo un risultato sub-ottimale ( valore 08 ). L'algoritmo hill climbing stocastico, invece, è in grado di esplorare in modo casuale anche la scelta secondaria 04, il cui cammino consente di raggiungere il nodo con valore 09 ( ottimo globale ). In conclusione, l'algoritmo hill climbing stocastico offre una maggiore completezza rispetto alla versione tradizionale dell'algoritmo.
 Tempo di elaborazione maggiore. L'esplorazione randomizzata è più completa ma anche meno efficiente. Dovendo elaborare un maggior numero di cammini a partire da un nodo corrente, l'algoritmo hill climbing stocastico giunge alla soluzione finale in modo più lento rispetto a un algoritmo stocastico. Ciò si verifica nella versione con eguali probabilità di scelta e, seppure in modo minore, anche nella versione con probabilità di scelta differenti. Per aumentare il livello di efficienza si ricorre alla versione simulated annealing in cui la probabilità delle scelte peggiorative decresce progressivamente nel corso del tempo di esecuzione dell'algoritmo.
Tempo di elaborazione maggiore. L'esplorazione randomizzata è più completa ma anche meno efficiente. Dovendo elaborare un maggior numero di cammini a partire da un nodo corrente, l'algoritmo hill climbing stocastico giunge alla soluzione finale in modo più lento rispetto a un algoritmo stocastico. Ciò si verifica nella versione con eguali probabilità di scelta e, seppure in modo minore, anche nella versione con probabilità di scelta differenti. Per aumentare il livello di efficienza si ricorre alla versione simulated annealing in cui la probabilità delle scelte peggiorative decresce progressivamente nel corso del tempo di esecuzione dell'algoritmo.
 Elevato numero di nodi vicini-successori. Nell'algoritmo hill climbing tradizionale sono analizzati tutti i nodi vicini al nodo corrente di riferimento. Quando i nodi vicini da analizzare sono molti l'algoritmo hill climbing potrebbe risentirne eccessivamente in termini di allungamento dei tempi di elaborazione. In questi casi particolari la versione stocastica è più veloce poiché consente di accelerare l'elaborazione mediante una scelta casuale tra tutti i nodi vicini disponibili senza doverli analizzare tutti.
Elevato numero di nodi vicini-successori. Nell'algoritmo hill climbing tradizionale sono analizzati tutti i nodi vicini al nodo corrente di riferimento. Quando i nodi vicini da analizzare sono molti l'algoritmo hill climbing potrebbe risentirne eccessivamente in termini di allungamento dei tempi di elaborazione. In questi casi particolari la versione stocastica è più veloce poiché consente di accelerare l'elaborazione mediante una scelta casuale tra tutti i nodi vicini disponibili senza doverli analizzare tutti.
