Ragionamento per assurdo
Il ragionamento per assurdo è un'argomentazione che a partire da un'ipotesi ( A ) e da un enunciato inconfutabilmente vero ( principio del terzo escluso ) giunge a una conclusione ( tesi ) impossibile o assurda. Il ragionamento per assurdo, o reductio ad absurdum, è un metodo utilizzato nelle dimostrazioni logico-matematiche. È conosciuto anche come dimostrazione per contraddizione o dimostrazione per refutazione. Supponendo di voler dimostrare che una proposizione A sia vera, il ragionamento per assurdo consiste nel partire da un'ipotesi in cui la proposizione A è falsa ( ¬ A ) e dimostrare che quest'ultima conduce a una contraddizione logica. In conclusione, se A non può essere falsa allora A deve essere vera. La dimostrazione per assurdo può essere formulata nel seguente modo:
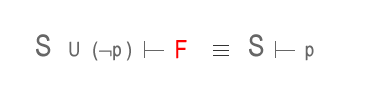
Dato un insieme S di proposizioni vere ( assiomi ) di riferimento e una proposizione logica p, se l'unione tra l'insieme S e la negazione della proposizione ( ¬ p ) conduce a una contraddizione logica F ( false ), allora la proposizione logica p segue logicamente l'insieme delle proposizioni S.
 Validità e soddisfacibilità. Nella logica proposizionale la relazione di validità e di soddisfacibilità di due proposizioni sono strettamente connesse. Se una proposizione A è valida, allora la negazione di A deve necessariamente essere insoddisfacibile. Allo stesso modo, se la negazione di A ( ¬ A ) è insoddisfacibile, allora la proposizione A deve essere necessariamente valida.
Validità e soddisfacibilità. Nella logica proposizionale la relazione di validità e di soddisfacibilità di due proposizioni sono strettamente connesse. Se una proposizione A è valida, allora la negazione di A deve necessariamente essere insoddisfacibile. Allo stesso modo, se la negazione di A ( ¬ A ) è insoddisfacibile, allora la proposizione A deve essere necessariamente valida.

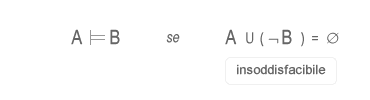
E' quindi possibile dimostrare B partendo da A, verificando l'insoddisfacibilità ( A ∧ ¬B ). Seguendo il ragionamento per assurdo, si ipotizza che la proposizione B sia falsa ( ¬B ). Se ( A ∧ ¬B ) è sempre falso ( insoddisfacibile ) allora A segue logicamente B. La dimostrazione per contraddizione può essere espressa nel seguente modo:

Dimostrazione per esaustione. Il metodo della dimostrazione per assurdo è un'alternativa al metodo classico per esaustione, in cui gli scienziati esplorano tutti i casi possibili per dimostrare la validità di un enunciato. Nella domostrazione per assurdo, invece, data una proposizione A, questa è valida se il suo contrario ( ¬ A ) implica un risultato falso rispetto al sistema logico-matematico di riferimento.
