Limite della funzione
Il limite studia l'andamento di una funzione matematica f(x) quando l'argomento (x) si avvicina a un determinato valore (x0).
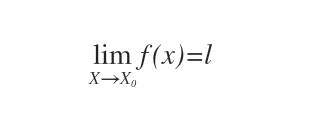
Definizione di limite. Si dice che la funzione f(x) tende al limite l per x tendente a x0, se dato un numero positivo qualsiasi ε è possibile determinare in corrispondenza ad esso un intorno (a, b) di x0, tale che per ogni x di (a,b) risulti l-ε<f(x)<l+ε tranne al più per il punto x0.
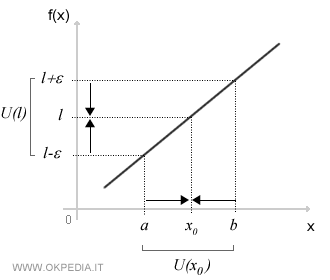
Spiegato più semplicemente, il limite della funzione f(x) per x tendente a x0 è l, se quanto più x si avvicina a x0, tanto più f(x) si avvicina a l.
Esempio di calcolo del limite
Prendiamo come esempio la funzione f(x)=x+1.
Ipotizziamo di voler calcolare il limite della funzione per x tendente a 4.
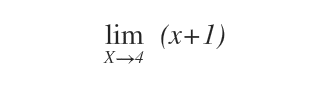
Nota. In questo caso X0 è uguale a 4.
Sappiamo che nel punto x0=4 la funzione f(x) è uguale a 5.
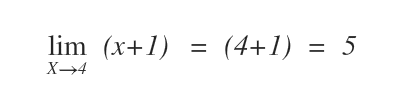
Pertanto il limite della funzione f(x) per x tendente a 4 è uguale a 5.
Dimostrazione:
Facciamo ora la verifica come richiede la definizione del limite.
Fissiamo un numero positivo qualsiasi ε e calcoliamo l'intorno del limite (5-ε,5+ε).
Ad esempio, se ε = 0.5 l'intorno del limite l è ( 4.5 , 5.5 ).
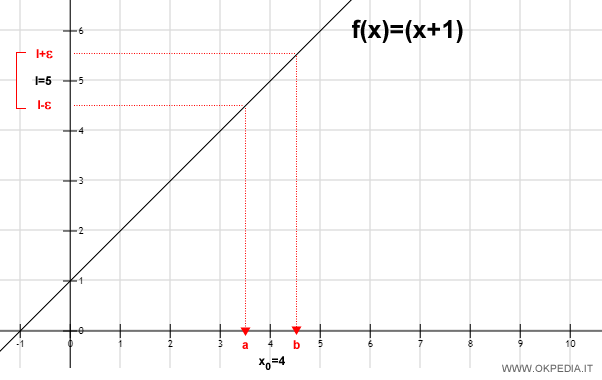
A partire dall'intorno (l-ε,l+ε) determiniamo l'intorno (a, b) di x0 ossia di x=4.
Per ogni valore della x nell'intorno (a, b) corrisponde a un valore della f(x) che appartiene all'intorno (5-ε,5+ε).
Questo soddisfa la definizione del limite e conferma che il limite della funzione f(x) per x tendente a 4 è effettivamente uguale a 5.
 Qual è l'utilità del limite della funzione? In questo semplice esempio di funzione reale e continua il calcolo del limite potrebbe sembrare inutile. Nel punto X0=4 la funzione è determinata e sappiamo già che f(x)=5. Si tratta di un caso volutamente semplice per far comprendere la definizione di limite. Il limite della funzione è particolarmente utile per studiare la funzione f(x) nei punti in cui è indeterminata.
Qual è l'utilità del limite della funzione? In questo semplice esempio di funzione reale e continua il calcolo del limite potrebbe sembrare inutile. Nel punto X0=4 la funzione è determinata e sappiamo già che f(x)=5. Si tratta di un caso volutamente semplice per far comprendere la definizione di limite. Il limite della funzione è particolarmente utile per studiare la funzione f(x) nei punti in cui è indeterminata.
L'origine del limite
Il concetto moderno di limite viene introdotto nella prima metà del '700 dal matematico francese D'Alembert. Poi migliorato dai matematici Cauchy ed Heine nel XIX secolo.
