A cosa serve il limite
Il limite di una funzione o successione è utile per studiare il comportamento di una funzione in un tratto non accessibile a partire dall'analisi dell'intorno, ossia dei dati nelle immediate vicinanze o di quelli tendenziali.
Quando è utile studiare il limite di una funzione?
Il limite della funzione è particolarmente utile per studiare il comportamento della funzione nei seguenti casi:
- nei punti in cui la funzione non esiste
Un esempio pratico è la divisione per zero. La funzione non è definita in questo punto. - nei punti in cui la funzione è indeterminata
Alcuni esempi pratici di forme di indecisione in matematica sono i seguenti:
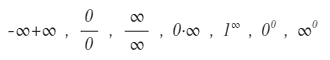
- nei punti per x tendente a infinito
L'insieme dei numeri reali è infinito a sinistra ( -∞) e a destra (+∞). Pertanto, non è possibile calcolare il valore iniziale e finale di una funzione continua. Si può però calcolare il limite
Ecco alcuni esempi pratici.
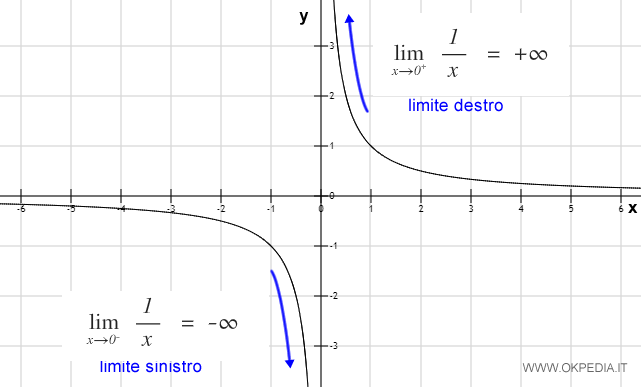
Il limite della divisione per zero
La seguente funzione non esiste per x=0 perché la divisione per zero non ha significato in matematico. Non è definita in questo punto.
Pertanto, per X=0 non è possibile calcolare un valore della funzione f(x).
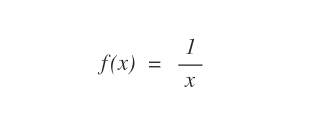
In questo caso, è utile calcolare il limite destro e sinistro della f(x) per x tendente a zero nell'intorno di X=0.
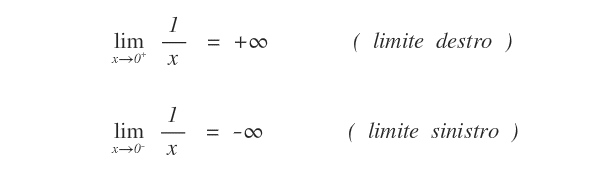
Si scopre così che la funzione tende a meno infinito (-∞) per x che tende a zero da sinistra ( limite sinistro ) e a più infinito (+∞) per x che tende a zero da destra ( limite destro).
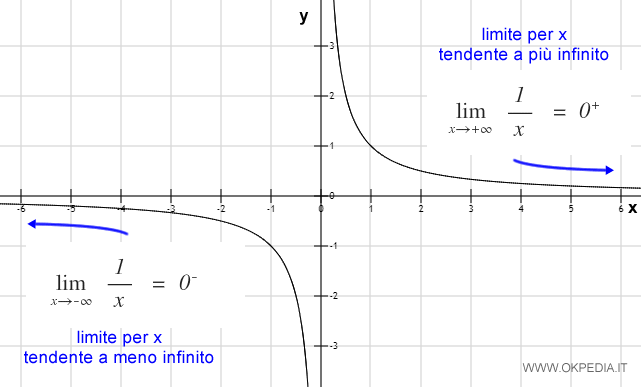
Il limite per infinito
Il dominio della seguente funzione è infinito ( -∞ , +∞ ).
Pertanto, la funzione non può essere calcolata agli estremi del dominio perché non esiste un valore minimo e massimo.
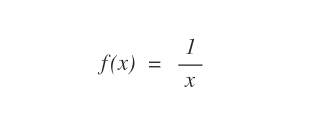
Per studiare il comportamento della funzione si può calcolare il limite per x tendente a più infinito ( +∞ ) e a meno infinito ( -∞ ).
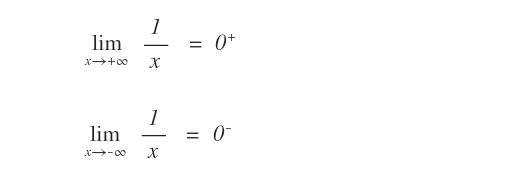
Grazie ai limiti infiniti si scopre che la funzione f(x) converge a 0+ per x tendente a più infinito ( +∞ ) e a 0- per x tendente a meno infinito ( -∞ )