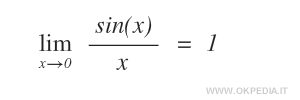Infinitesimi

Si dice infinitesimo per x→c il limite di una funzione f(x) che tende a zero, dove c è numero finito o infinito.

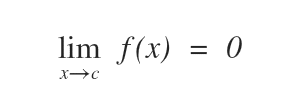
Esempio. La seguente funzione è un infinitesimo perché il limite della funzione tende a zero per x→∞.

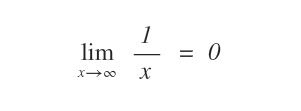
Gli infinitesimi simultanei

Gli infinitesimi simultanei sono due o più funzioni f(x), g(x), ... , z(x) che tendono a zero per lo stesso valore x→c.

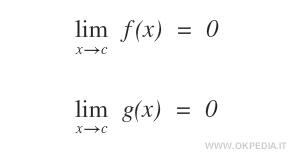
A cosa servono gli infinitesimi?

Nel calcolo infinitesimale il confronto tra due infinitesimi consente di calcolare il limite più rapidamente.

Esempio. Il limite del prodotto di due infinitesimi simultanei f(x)·g(x) è determinato dal fattore che tende a zero più velocemente rispetto all'altro.

Analizzando il grafico delle due funzioni si può notare come (x-1)² tenda a zero più velocemente rispetto a (x-1) nell'intorno x=1.

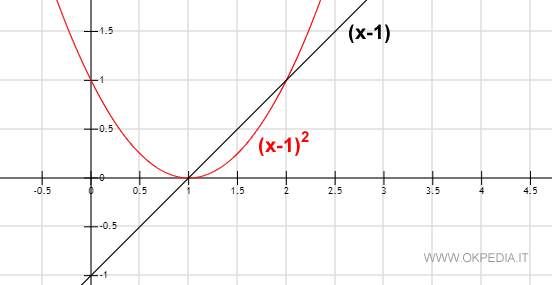
Il confronto tra infinitesimi

Per confrontare due infinitesimi si studia il limite del rapporto tra due funzioni f(x)/g(x).

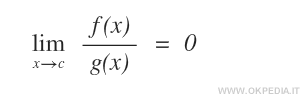
Nota. Nel confronto si presuppone che esista un intorno I di c tale che g(x)≠0 per ogni x∈I e x≠c.

Il risultato del confronto è classificabile in uno dei seguenti casi:

• Infinitesimo di ordine superiore. La funzione f(x) è un infinitesimo di ordine superiore quando il limite del rapporto f(x) / g(x) per x→c è uguale a zero. La funzione f(x) tende a zero più velocemente rispetto a g(x).
  

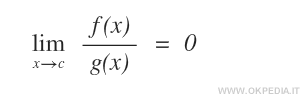
  Nota. Se la funzione f(x) è un infinitesimo di ordine superiore rispetto a g(x) allora la funzione g(x) è un infinitesimo di ordine inferiore rispetto a g(x).

• Infinitesimo dello stesso ordine. Le funzioni f(x) e g(x) sono dette infinitesimi dello stesso ordine quando il limite del rapporto f(x) / g(x) per x→c è uguale a un numero l finito e diverso da zero. Le due funzioni convergono a zero con la stessa rapidità.
  
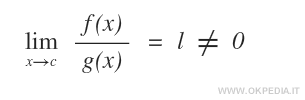
• Infinitesimo di ordine inferiore. La funzione f(x) è un infinitesimo di ordine inferiore quando il limite del rapporto f(x) / g(x) per x→c è uguale a ± infinito. La funzione f(x) tende a zero più lentamente rispetto a g(x).
  

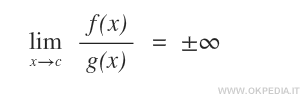
  Nota. Se la funzione f(x) è un infinitesimo di ordine inferiore rispetto a g(x) allora la funzione g(x) è un infinitesimo di ordine superiore rispetto a g(x).

• Infinitesimi non confrontabili. Le funzioni f(x) e g(x) sono dette infinitesimi non confrontabili se non esiste il limite del rapporto f(x) / g(x) per x→c.
  

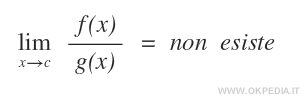
Esempi di infinitesimi simultanei

Nel seguente rapporto (x-1)² è un infinitesimo di ordine superiore rispetto a (x-1) per x→1.

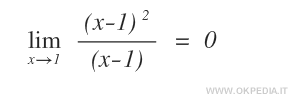
Allo stesso modo si può dimostrare che (x-1) è un infinitesimo di ordine inferiore rispetto a (x-1)² per x→1.

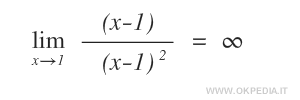
Nel caso delle funzioni sin(x) e x, invece, si tratta di due infinitesimi dello stesso ordine per x→0.