Ricerca ad approfondimento iterativo
La ricerca ad approfondimento iterativo è un metodo di ricerca non informato. L'algoritmo di ricerca ad approfondimento iterativo effettua le operazioni di ricerca in ampiezza, aumentando progressivamente il valore di taglio ( profondità ) dell'albero logico ad ogni ciclo di ricerca ( iter ). In altri termini, inizialmente l'algoritmo effettua le operazioni di ricerca nei nodi poco profondi, quelli vicini al nodo radice, aumentando progressivamente la profondità di scansione nei cicli di ricerca successivi. Nel momento in cui l'algoritmo trova una soluzione interrompe il ciclo di ricerca senza dover scandagliare ulteriormente l'albero logico alla ricerca di altre soluzioni. La sequenza di ricerca dell'algoritmo è la seguente:
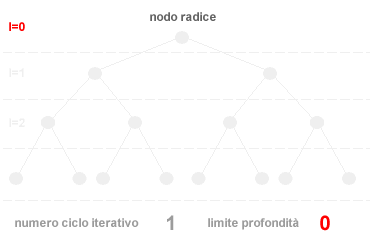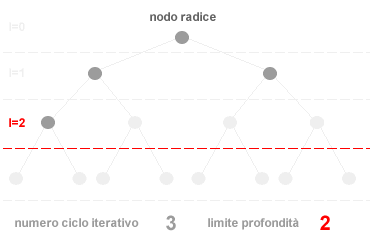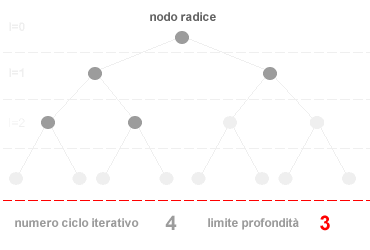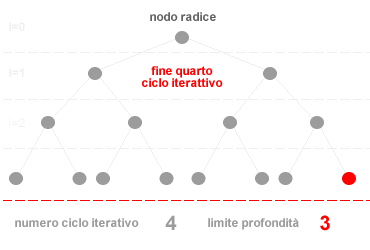
La strategia di ricerca ad approfondimento è, pertanto, un algoritmo che integra in sé sia la ricerca in ampiezza che la ricerca in profondità. L'algoritmo esplora i primi livelli dei nodi prima di passare ai livelli successi. Se la soluzione è situata nei primi livelli dell'albero logico la ricerca ad approfondimento iterativo è più efficiente di una ricerca in profondità poiché evita di scandagliare ogni ramo in profondità e di consumare una grande quantità di memoria. Tra un ciclo iterativo e l'altro è sufficiente mantenere in memoria soltanto la variabile relativa al valore di taglio ossia al numero che identifica limite di profondità della ricerca. Una volta raggiunto tale limite, l'algoritmo aumenta il valore di taglio, azzera la memoria e ricomincia daccapo una nuova ricerca con un livello di profondità più elevato. Data un fattore di ramificazione b e una profondità d la complessità temporale dell'algoritmo è la seguente:
(d)b + (d-1)b2 + .... + 1(bd)
La ripetizione dei nodi iniziali in ogni iter influisce poco sulla complessità dell'algoritmo poiché gran parte della quantità dei nodi di un albero di ricerca si trovano nei rami più in profondità. L'algoritmo di ricerca ad approfondimento iterattivo può, inoltre, svuotare la memoria ad ogni ciclo (iter) di ricerca. Essendo la ripetizione dei nodi iniziali poco influenti sulla complessità la complessità dell'algoritmo può essere approssimata in O(bd). Pur essendo più complesso rispetto ad una ricerca in ampiezza, rispetto a quest'ultima l'algoritmo di ricerca in profondità consente di gestire in modo più razionale la quantità di memoria a disposizione. È quindi utile quando lo spazio di ricerca è molto vasto e non si conosce con precisione il fattore di ramificazione dell'albero di ricerca.
- Nota di un lettore. L'algoritmo spiegato qui è sbagliato. Il grafico spiega un algoritmo in ampiezza che viene ripetuto livello dopo livello, in realtà viene ripetuto un algoritmo in profondità, perché altrimenti non avrebbe senso ripetere tante volte un algoritmo in ampiezza con, ogni volta, un livello in più.... tanto vale sarebbe fare solo l'ultima iterazione. 10/03/2015
