Ricerca in ampiezza
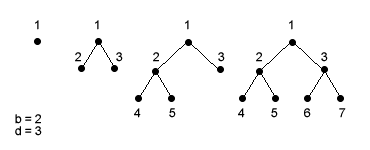
La ricerca in ampiezza è una ricerca non informata in cui i nodi dell'albero logico (dati) sono analizzati seguendo un ordine di vicinanza al nodo radice. Sono espansi dapprima i nodi più vicini alla radici, ad esempio da sinistra verso destra, e successivamente tutti gli altri nodi successori fino ad una profondità d. Da un punto di vista formale ogni nodo successore viene aggiunto alla coda FIFO ( First Input First Output ) dei nodi ancora da analizzare non appena viene espanso. La strategia di ricerca in ampiezza si interrompe nel momento in cui trova la prima soluzione. Per semplicità espositiva, nello spazio degli stati seguente è indicato l'ordine di esplorazione dei nodi. Il nodo radice 1 è il primo ad essere esplorato, il nodo successore 2 è il secondo, il nodo 3 successore è il terzo ecc. Per ogni esplorazione vengono individuati i nodi figli (es. 4 e 5) e aggiunti in coda nella lista aperta dei nodi ancora da esplorare.
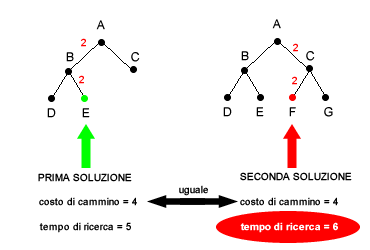
La ricerca in ampiezza è ottimale quando il costo di passo è ovunque uguale per ogni arco ed è in funzione non decrescente della profondità dell'albero di ricerca Questa condizione consente di affermare con certezza che la prima soluzione trovata è anche la migliore. Se anche ci fosse un'altra soluzione allo stesso livello di profondità avrebbe un costo di cammino identico alla precedente. Ad esempio, dato un costo di passo pari a 2 e due soluzioni possibili E e F, entrambe hanno un medesimo costo di cammino, pari a 4, ma la prima soluzione ad essere trovata (nodo E) vanta un tempo di ricerca inferiore rispetto alla seconda soluzione (nodo F). Quando l'algoritmo giunge alla prima soluzione (nodo E) può pertanto interrompere il ciclo di ricerca e restituire la soluzione.
La complessità della ricerca in ampiezza è in funzione esponenziale della profondità dei nodi (d) e del fattore di ramificazione (b). Il numero massimo dei nodi espansi è pari a O(bd) dove la notazione O equivale a dire "al più uguale a".
O(bd) = 1 + b1 + b 2 + ... + bd-1
Ad esempio, nello spazio degli stati precedente il fattore di ramificazione b (branching factor) è pari a 2, il livello di profondità d (depth) è pari a 3. Ciò equivale a dire che il massimo dei nodi espansi dello spazio degli stati è pari a 1 + 21+22 = 1 + 2 + 4 = 7 ossia "al più uguale a" 23 =8 .
 Complessità dell'algoritmo. La ricerca in ampiezza è penalizzata quando lo spazio degli stati ha un elevato fattore di ramificazione (b) e/o un elevato livello di profondità (d). Dovendo memorizzare ogni nodo espanso (successore) nella lista aperta, è necessario disporre di adeguati requisiti di memoria ( complessità spaziale ) e mettere in conto un tempo di esecuzione molto lungo ( complessità temporale ). In casi estremi, il tempo di elaborazione potrebbe essere eccessivo, facendo perdere ogni utilità pratica alla ricerca. Ad esempio, se l'algoritmo fosse in grado di analizzare 1000 nodi al secondo, ci vorrebbero comunque circa 35 anni di elaborazione per analizzare un albero di ricerca con fattore di ramificazione k=12 e di profondità d=12. Potrebbero, inoltre, non esistere al mondo dispositivi hardware con sufficiente capacità di memoria in grado di supportare l'esecuzione dell'algoritmo di ricerca.
Complessità dell'algoritmo. La ricerca in ampiezza è penalizzata quando lo spazio degli stati ha un elevato fattore di ramificazione (b) e/o un elevato livello di profondità (d). Dovendo memorizzare ogni nodo espanso (successore) nella lista aperta, è necessario disporre di adeguati requisiti di memoria ( complessità spaziale ) e mettere in conto un tempo di esecuzione molto lungo ( complessità temporale ). In casi estremi, il tempo di elaborazione potrebbe essere eccessivo, facendo perdere ogni utilità pratica alla ricerca. Ad esempio, se l'algoritmo fosse in grado di analizzare 1000 nodi al secondo, ci vorrebbero comunque circa 35 anni di elaborazione per analizzare un albero di ricerca con fattore di ramificazione k=12 e di profondità d=12. Potrebbero, inoltre, non esistere al mondo dispositivi hardware con sufficiente capacità di memoria in grado di supportare l'esecuzione dell'algoritmo di ricerca.
