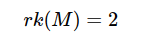Teorema di Kronecker
Il teorema di Kronecker (o teorema degli orlati) è un teorema di algebra lineare che permette di calcolare il rango di una matrice.
- Il rango di una matrice M è uguale a k se e solo se
- esiste un minore non nullo A di ordine k
- tutti i minori di ordine k+1 ottenuti orlando il minore A sono nulli.
Cosa significa orlare un minore? Orlare un minore vuol dire aggiungere al minore A una riga e una colonna della matrice M.
Il teorema degli orlati riduce le operazioni di calcolo del rango perché si limita a studiare i soli orlati di ordine k+1 del minore A.
Esempio
Calcolare il rango della matrice M
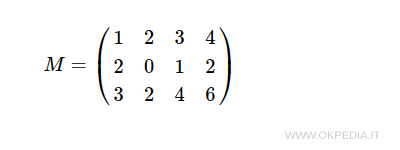
Il rango della matrice è compreso tra 1 e 3 perché è una matrice 3x4
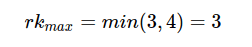
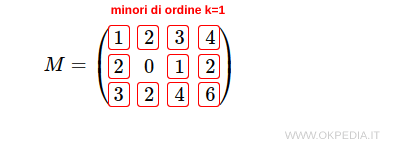
La matrice ha diversi minori di ordine k=1.
Ogni elemento non nullo della matrice (es. 1, 2, 3, ecc. )è un minore di ordine k=1.
La matrice ha diversi minori di ordine k=2.
Consideriamo il minore A
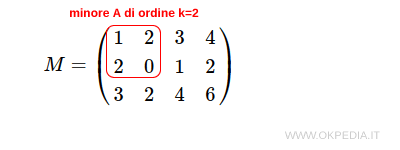
Il minore A è un minore di ordine k=2
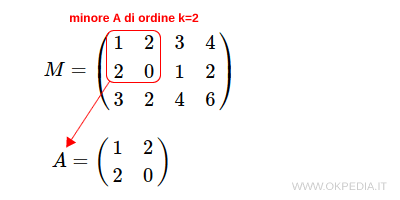
E' un minore non nullo perché il determinante è diverso da zero
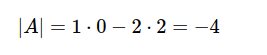
Gli orlati possibili del minore A sono due
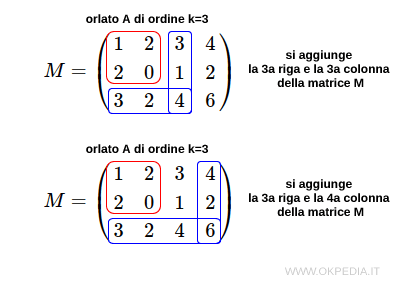
Gli orlati del minore A sono B1 e B2

Calcoliamo il determinante degli orlati
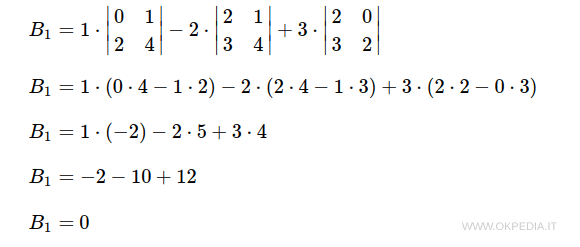
E' un minore nullo. Pertanto, si procede a verificare anche l'altro minore.
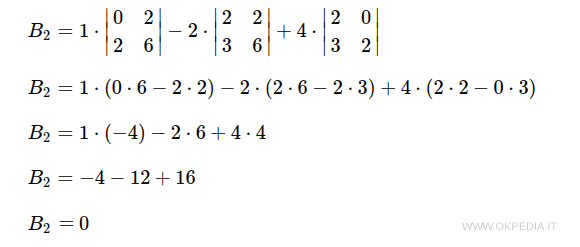
Entrambi i minori orlati di A di ordine 3 (k+1) sono nulli.
Pertanto, secondo il teorema di Kronecker il rango della matrice è uguale a due.