Come calcolare la Singular Value Decomposition (SVD) di una matrice

Quando si parla di SVD si intende la decomposizione ai valori singolari di una matrice. Qualsiasi matrice algebrica è equivalente al prodotto di altre tre matrici, opportunamente calcolate seguendo il procedimento SVD. In pratica, se hai una matrice A di dimensioni mxn ( m colonne, n righe ), la forma SVD equivalente è il prodotto di una matrice USVT. La tabella U ha un dimensione mxm, la matrice S è di dimensioni mxn ed è di pari dimensioni rispetto alla matrice A, mentre la matrice VT è di dimensioni nxn.

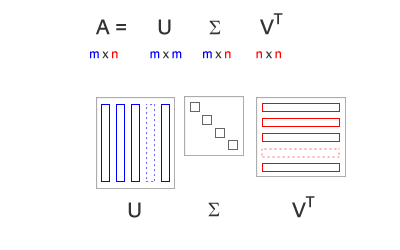
Per comprendere come ottenere le tre tabelle SVD ti consiglio di partire da un esempio pratico. Prendi una semplice tabella, una tabella quadrata di piccole dimensioni ( 2x2 ) come la seguente:

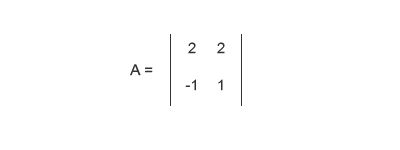
A questo punto, prima di iniziare, calcola la matrice trasposta A^T. Come vedrai ci servirà per calcolare le matrici SVD. Una matrice trasposta si ottiene sostituendo le righe con le colonne della matrice A.

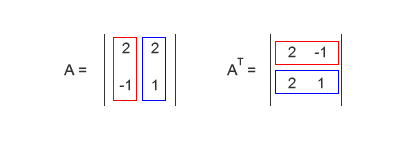
Moltiplica la matrice trasposta A^T per la matrice di origine A, ottenendo come risultato la matrice A^TA.

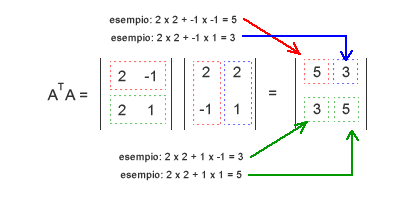
La matrice A^TA ti permette di calcolare gli autovalori, come prima cosa devi calcolare il polinomio caratteristico della matrice A^TA. Puoi ottenere il polinomio caratteristico calcolando la differenza tra la matrice A^TA e una matrice identica I_d moltiplicata per una variabile incognita λ. Fai attenzione, per matrice identica ( o identità ) si intende una matrice con il valore uno sulla diagonale e zero in tutto il resto.

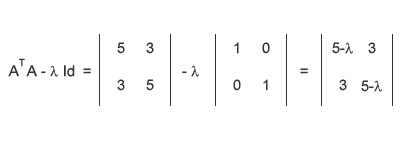
Il determinante della matrice A^TA-λId ti consente di ottenere il polinomio caratteristico della matrice.

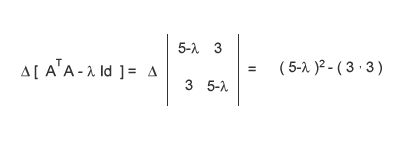
A cosa serve il polinomio caratteristico? Ti consente di calcolare gli autovalori della matrice. Poni a zero il polinomio e trova i valori della variabile λ che soddisfano l'equazione. Dopo qualche semplice passaggio algebrico, ottieni un'equazione di secondo grado che viene risolta con i valori λ=2 e λ=8 detti autovalori.

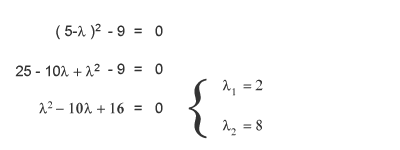
Gli autovalori λ=2 e λ=8 ti sono molto utili, poiché ti consentono di ottenere la matrice Σ i cui componenti sono uguali alla radice degli autovalori della matrice. Ti ricordo che la matrice Σ ha una dimensione pari alla matrice A, lo stesso numero mxn di colonne (m) e di righe (n), e i suoi elementi occupano soltanto la diagonale mentre tutti gli altri sono pari a zero.

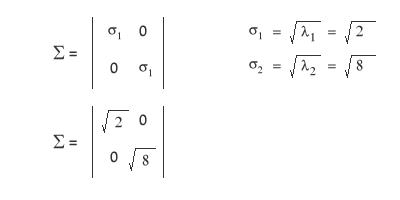
Gli autovalori ti consentono anche di ottenere un'altra matrice SVD ma prima devi svolgere qualche calcolo aggiuntivo. Ora conosci gli autovalori ( λ=2 e λ=8 ) ma non conosci ancora gli autovettori di A^TA. Torna alla matrice A^TA-λId e trasforma le due righe in due equazioni pari a zero. I valori della matrice sulla prima colonna moltiplicano la variabile x mentre quelli della seconda colonna la variabile y.

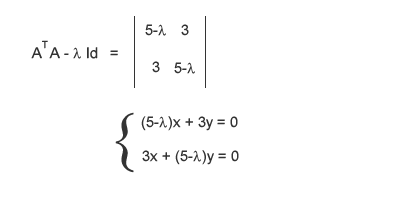
Per calcolare il primo autovettore, sostituisci λ=2 e trova una soluzione al sistema di equazioni. Risolvendo il sistema di equazioni puoi trovare i valori delle coordinate x e y, ossia i valori del primo autovettore V₁.

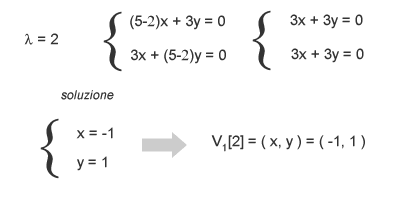
Per calcolare il secondo autovettore devi ricostruire il sistema di equazioni a partire dall'altro autovalore, ossia λ=8 e trovare le altre coordinate x, y. Hai trovato il secondo autovettore V₂.

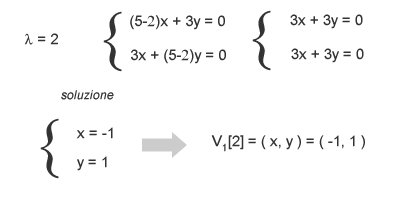
Ricapitolando, hai trovato i due autovettori V₁ e V₂ che ti sono utili per scrivere la matrice V^T. Per calcolare V^T devi prima normalizzare gli autovalori. In pratica, devi dividere ogni elemento dei vettori V₁ e V₂ per la rispettiva norma. La norma è la radice quadrata della somma del quadrato dei valori degli elementi.

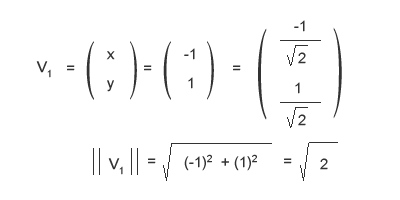
Ripeti la stessa operazione per normalizzare l'autovettori V₂ per la rispettiva norma.

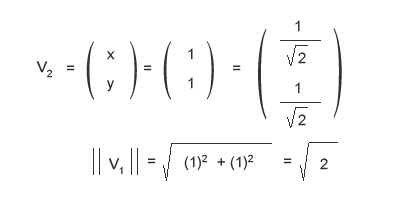
Con i due vettori normalizzati V₁ e V₂ puoi finalmente ottenere la matrice V^T.

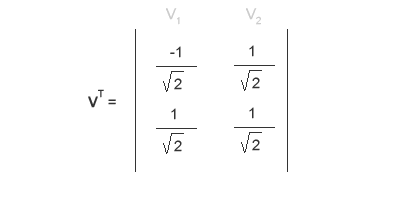
A questo punto ti manca soltanto una matrice per completare la SVD. Puoi calcolarla seguendo lo stesso procedimento fin qui svolto ma a partire AA^T anziché dalla A^TA. Puoi però raggiungere lo stesso risultato utilizzando questa semplice regola:

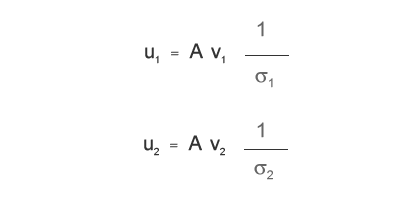
Il primo autovettore (u₁) della tabella U è determinato dal prodotto della matrice A con l'autovettore v₁ moltiplicato per il reciproco del primo autovalore. Detta così può sembrare difficile ma, sicuramente, qualsiasi tuo dubbio sarà chiarito guardando il procedimento di seguente calcolo in cui ho svolto ogni singolo passaggio algebrico passo dopo passo:

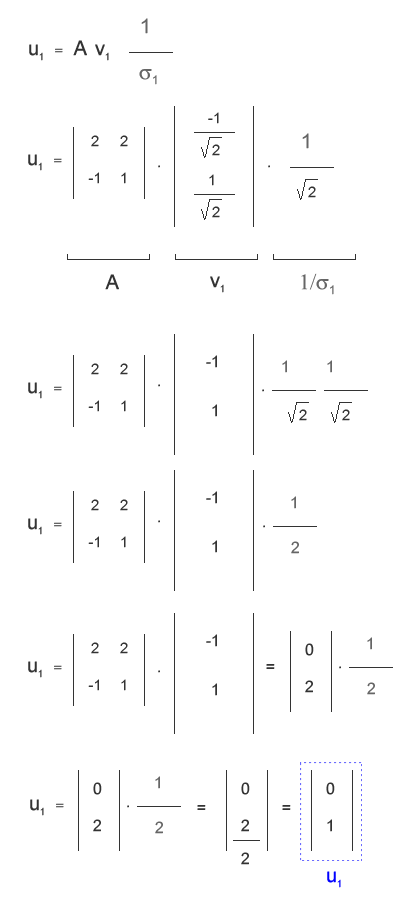
Hai trovato il primo autovettore u₁ della matrice U. Utilizzando lo stesso metodo puoi calcolare anche l'altro autovettore u₂. Nella figura che segue ho omesso di svolgere tutti i passaggi nel dettaglio ma, guardando il precedente esempio, dovresti aver già capito il funzionamento.

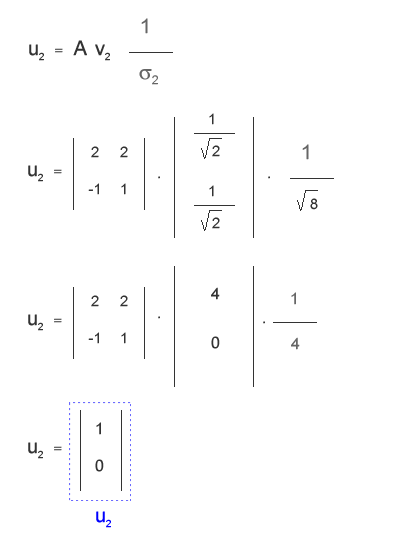
Hai calcolato entrambi gli autovettori u₁ e u₂ di U che, in questo caso, è una matrice quadrata. Mettendo in colonna i due autovettori puoi scrivere la matrice U per intero.

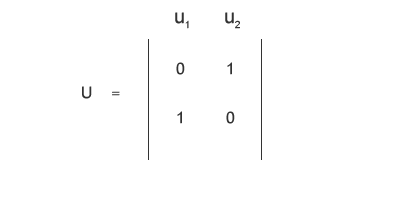
Con la matrice U hai ottenuto tutte le componenti della forma UΣV^T equivalente alla matrice A che riscrivo qui di seguito per concludere questo esercizio.

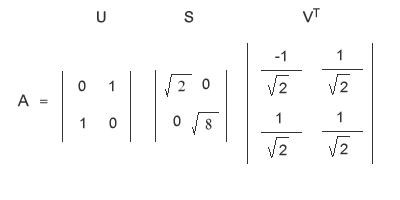
Questo tutorial potrà sembrare banale a chi sa già svolgere questi calcoli e possiede sufficiente dimestichezza con il calcolo algebrico. Ho svolto questa esercitazione pensando a chi si trova per la prima volta dinnanzi al calcolo della decomposizione dei valori singolari ( SVD ) di una matrice, magari con qualche lacuna in algebra vettoriale, per potergli spiegare, passo dopo passo, il funzionamento. Una volta compreso lo svolgimento di un esempio pratico, diventa più semplice studiare e capire la teoria.