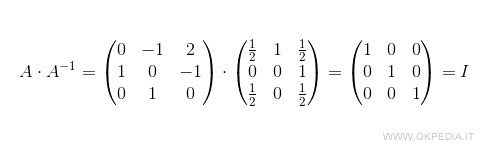Matrice inversa
La definizione di matrice inversa
Sia A una matrice quadrata di ordine n. Se esiste, la matrice inversa A-1 è una matrice quadrata tale che A·A-1=I e A-1·A=I, dove I è la matrice identità di ordine.
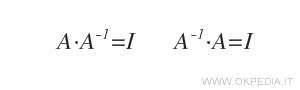
Se esiste la matrice inversa A-1, la matrice A è detta matrice invertibile o non singolare.
Viceversa, se non esiste la matrice inversa, la matrice A è detta non invertibile o singolare.
Nota. Se la matrice inversa di A esiste, allora la matrice inversa A-1 è unica.

Come calcolare la matrice inversa
Una matrice quadrata è invertibile se il suo determinante è diverso da zero.
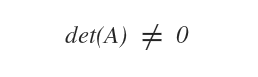
Se la matrice è invertibile, si può calcolare la sua matrice inversa tramite il teorema di Laplace.
La matrice inversa A-1 di una matrice quadrata A di ordine n con determinante diverso da zero è la trasposta della matrice dei complementi algebrici A'T divisa per il determinante |A|.
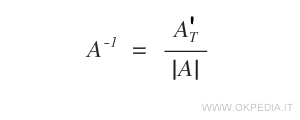
Un esempio di calcolo
Data la matrice quadrata A di ordine 3
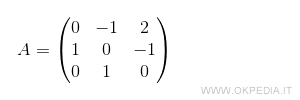
Il determinante della matrice A è uguale a 2.
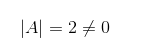
Quindi, la matrice A è una matrice invertibile. Si può calcolare la matrice inversa.
Calcoliamo la matrice dei complementi algebrici A' ( o matrice dei cofattori ).

Poi calcoliamo la trasposta della matrice dei complementi algebrici.
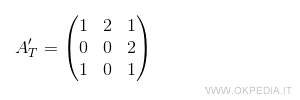
Dividendo la trasposta A'T per il determinante |A| si ottiene la matrice inversa di A.
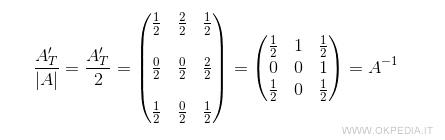
Pertanto, la matrice inversa A-1 è la seguente:
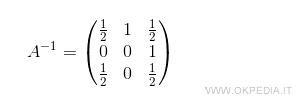
Verifica. Per verificare il risultato, basta moltiplicare la matrice A per la matrice inversa A-1. Il prodotto A·A-1 è la matrice identità I ossia una matrice con gli elementi della diagonale uguali a 1 e tutti gli altri uguali a zero.