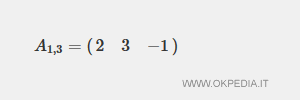Matrice
Una matrice è una tabella con p righe e q colonne. I numeri p e q sono interi positivi che definiscono le dimensioni (p,q) della matrice. Una matrice si indica con Mpxq o M(p,q).
Le matrici sono indicate con il simbolo di una lettera maiuscola, seguita eventualmente dalle dimensioni della matrice.
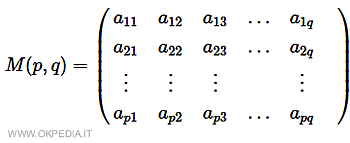
Ogni elemento ( o coefficiente ) aij situato in corrispondenza della coppia (i,j) della matrice è un numero reale che si trova in corrispondenza dell'incrocio di ogni i-esima riga e j-esima colonna.
Tipo di coefficienti. Per definire il tipo di coefficienti nella matrice si aggiunge un'ulteriore parametro alle dimensioni che indica l'insieme di riferimento. M(p,q,I). Ad esempio, l'insieme delle matrici pxq con coefficienti reali ℜ si indica M(p,q,ℜ). Una matrice A appartenente all'insieme delle matrici reali si indica con A ∈ M(p,q,ℜ)
Esempio
Questa matrice è composta da due righe e tre colonne.
Le dimensioni della matrice sono p=2 e q=3.
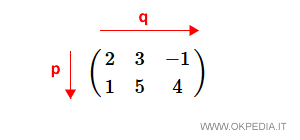
Gli elementi aij della matrice sono

La matrice si indica con una lettera maiuscola seguita eventualmente dalle dimensioni
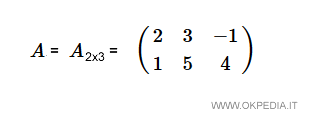
La matrice A appartiene all'insieme delle matrici M(2,3) di dimensioni 2x3.
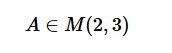
Matrici quadrate e rettangolari
Le dimensioni p e q della matrice definiscono il tipo di matrice
- Matrice quadrata. È una matrice con uguale numero di righe (p) e di colonne (q).
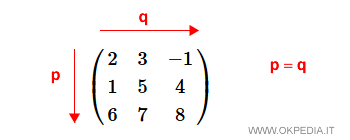
- Matrice rettangolare. È una matrice con un numero diverso di righe (p) e di colonne (q).
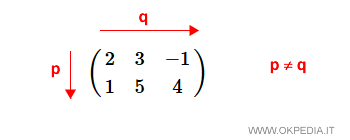
Casi particolari della matrice rettangolare sono la matrice colonna e la matrice riga.
1] La matrice colonna è composta da una sola colonna (q=1)
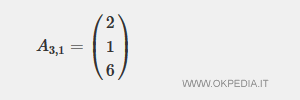
2] La matrice riga è composta da una sola riga (p=1)