Come calcolare gli autovalori di una matrice
Hai una matrice e devi calcolare gli autovalori ma non sai come fare. A volte la teoria può essere ostica, se non si comprende subito, e non c'è niente di meglio di un esempio per capire. Prendi una qualsiasi matrice a tuo piacimento, in questo esempio io utilizzo una matrice a 3 dimensioni.
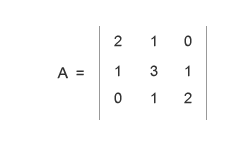
Data una matrice A, puoi calcolare i suoi autovettori eguaglando a zero il suo polinomio caratteristico. Come prima cosa devi costruire individuare la matrice identica di A, una matrice identica ha pari dimensioni rispetto a quella di origine e presenta come elementi il valore uno ( 1 ) sulla diagonale e lo zero ( 0 ) in tutte le altre celle. A volte viene chiamata anche matrice identità, è sempre la stessa cosa. Qui di seguito puoi vedere la matrice Id che è un esempio di matrice identica della matrice A. Come puoi subito notare, è caratterizzata da una sequenza di 1 sulla diagonale e valori nulli nel resto della matrice.
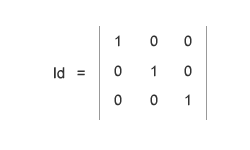
Nel passo successivo devi calcolare la matrice ( A - λ Id ) dove lambda ( λ ) è una variabile incognita. Si tratta di una matrice di pari dimensioni pari alla differenza tra ogni elementio della matrice A e ogni elemento della matrice Id moltiplicato per lambda ( λ ). La matrice identica ha valori positivi soltanto nella diagonale, quindi devi modificare soltanto la diagonale della matrice A, la zona che qui di seguito ho colorato in blu.

la matrice ( A - λ Id ) non è altro che la matrice A a cui aggiungi la sottrazione della variabile lambda ( λ ) nella diagonale. A questo punto, calcolando il determinante della matrice ( A - λ Id ) ottieni il polinomio caratteristico della matrice A.
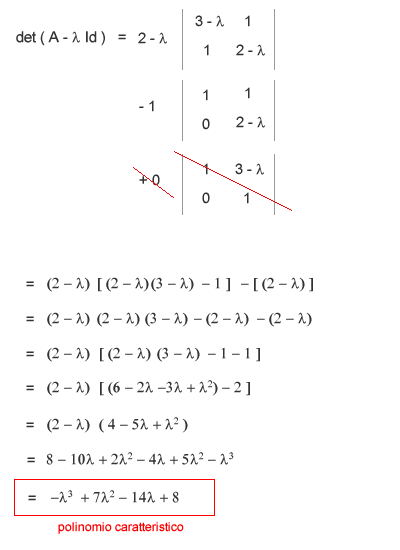
Una volta trovato il polinomio caratteristico lo eguagli a zero e puoi così trovare i valori di lambda ( λ ) che soddisfano l'equazione ossia i gli autovalori. Nel caso precedente, la soluzione è molto semplice poiché puoi scomporre il polinomi caratteristico con la regola di Ruffini per trovare le radici reali.
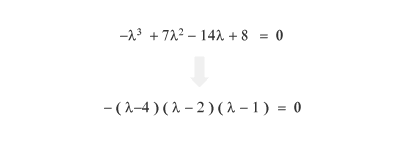
La precedente equazione è uguale a zero quando lambda è uguale a quattro ( λ=4 ), a due ( λ=2 ) oppure a uno ( λ=1 ). Questi valori di lambda sono gli autovalori della matrice A. Hai trovato gli autovalori della matrice.
