Come calcolare gli autospazi e gli autovettori di una matrice
Hai una matrice e devi calcolare gli autovettori e gli autospazi di una matrice ma non sai proprio da dove iniziare. Un modo per capire il funzionamento di una cosa è partire da un esempio, una volta capita la meccanica della risoluzione diventa più facile studiare e ricordare la teoria. Prendi una qualsiasi matrice, io ho preso la seguente matrice ( A ) perché abbastanza semplice da risolvere:
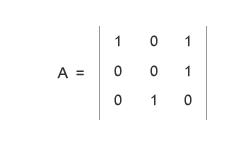
Il primo passo che devi fare è calcolare gli autovalori della matrice. In pratica, senza rivedere come si calcolano gli autovalori.come calcolare gli autovalori di una matrice, sottrai una variabile incognita ( λ ) dagli elementi situati sulla diagonale della matrice A.
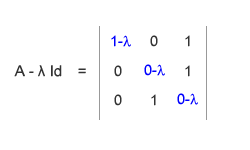
La precedente matrice la chiamo ( A - λ Id ). Questa matrice ci consente di ottenere il polinomio caratteristico della matrice A. Come si fa? Calcola il determinante della matrice ( A - λ Id ) ed eguaglialo a zero, hai ottenuto il polinomio caratteristico della matrice.

L'equazione del polinomio caratteristico ha due soluzioni, e si vedono facilmente, l'equazione diventa uguale a zero quando la variabile lamda è uguale a uno ( λ = 1 ) oppure quando è uguale a meno uno ( λ = -1 ). Questi due risultati sono dette autovalori della matrice. A questo punto puoi procedere con il calcolo degli autovalori e dell'autospazio. La matrice può essere trasformata in un sistema lineare a tre variabili ( x, y, z ) come nella seguente figura.

Parti dall'ipotesi ( λ = 1 ) e sostituisci nel sistema lineare, in questo modo puoi studiare il primo autovettore. Quest'assegnazione trasforma il sistema lineare nella seguente forma:
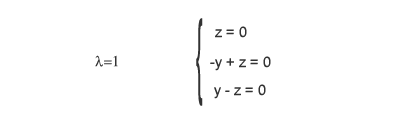
Il sistema lineare costruito con l'ipotesi λ = 1 ha una sola soluzione, tutte le equazioni sono uguali a zero quando la variabile z è uguale a zero ( z=0 ) e la variabile y è uguale a zero ( y = 0 ). Hai ottenuto le prime coordinate (x,y,z) sullo spazio ossia il primo autovettore della matrice che puoi scrivere nel seguente modo:
V[1] = (1,0,0)
Come puoi notare, alla variabile x io ho scelto di assegnare il valore uno ( x = 1 ) ma si tratta di una scelta arbitraria. Ciò che conta è aver ottenuto un punto nello spazio a tre dimensioni a partire dal sistema. La dimensione dell'autospazio è pari a uno, essendo generato da un vettore. A questo punto, puoi ripetere la stessa operazione analizzando il sistema lineare con l'ipotesi λ = 2.
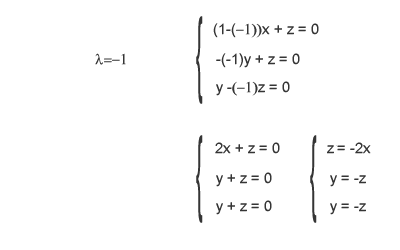
Il secondo sistema lineare viene risolto quando la variabile z è uguale a -2x e la variabile y è uguale a -z ossia, il che è lo stesso, è uguale a 2x. Hai ottenuto altre due coordinate (y,z) ossia ( 2x, -2x ). In precedenza, se ricordi bene, ho assegnato a caso alla variabile x il valore uno (x=1), considerando anche questo valore puoi calcolare il secondo autovettore che, in questo caso, è il seguente:
V[-1] = (1,2,-2)
Il secondo autovettore ha una dimensione di autospazio pari a uno poiché dipende da un solo vettore. Hai ottenuto i due autovettori della matrice.
