Ricerca in profondità limitata
La ricerca in profondità limitata è un algoritmo di ricerca non informata. La ricerca si svolge per ogni singolo ramo dell'albero di ricerca in verticale sui nodi-figli fino ad una determinata profondità ( depth ) oltre il quale l'algoritmo passa ad analizzare il successivo ramo o cammino. Dal punto di vista formale il limite di profondità è un limite al numero dei passi per ogni cammino. Ad esempio, dato un albero di ricerca con fattore di ramificazione pari a due (b=2), profondità pari a cinque (d=5) e limite di profondità pari a quattro (l=4), possiamo rappresentare l'albero di ricerca indicando per ogni nodo il relativo ordine di elaborazione.
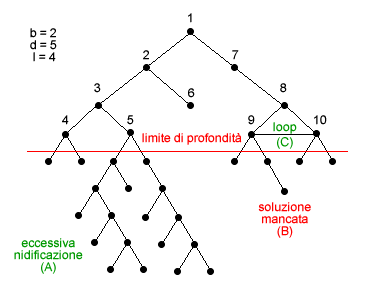
La ricerca in profondità limitata si distingue dall'algoritmo classico di ricerca in profondità per la minore complessità spaziale e temporale dell'algoritmo. Come si può facilmente osservare seguendo l'ordine numerico di elaborazione, il processo di ricerca lungo ogni ramo si interrompe al raggiungimento del limite di profondità ( taglio di ricerca ) senza espandere ulteriori nodi figli. Ciò consente di ridurre il rischio di incappare nell'eccessiva nidificazione di un ramo a scapito degli altri ( caso A ) e di evitare il rischio dei "loop" ossia dei cicli reiterati ed infiniti ( caso C ).
Soluzioni in profondità. D'altra parte l'algoritmo ricerca in profondità limitata riduce anche le possibilità di trovare la soluzione al problema, in particolar modo quando si tratta di soluzioni in profondità. Ad esempio, il nodo (B) nell'albero di ricerca è una soluzione al problema ma, essendo al di sotto del taglio di profondità, non sarà mai trovata dall'algoritmo di ricerca. In conclusione, la ricerca in profondità è efficace ( completa ) soltanto nei casi in cui le soluzioni siano superficiali ossia concentrate negli strati superficiali dell'algoritmo di ricerca.
